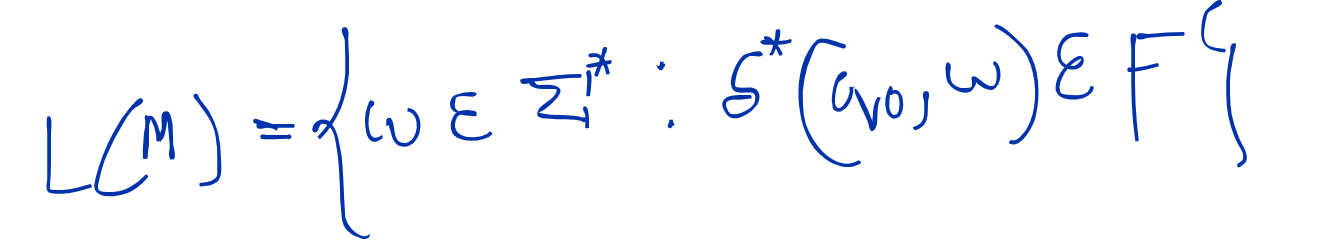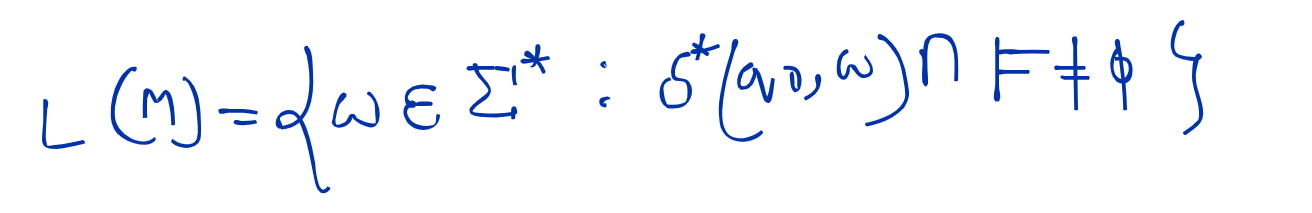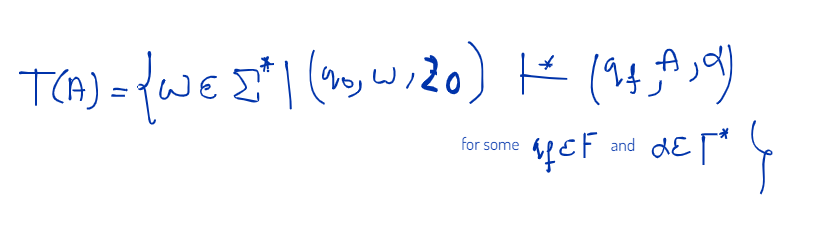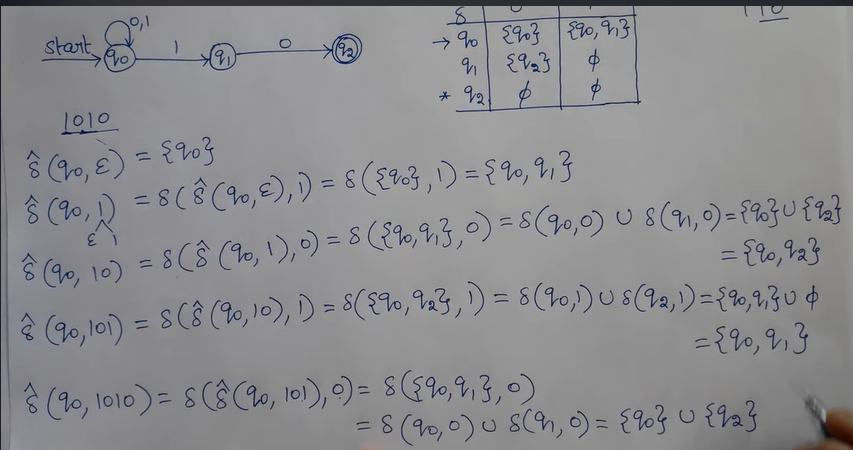TOC

• What do you mean by theory of computation ? Discuss about it's branches ?
  • The theory of computation is a field of computer science that deals with the study of algorithms, formal languages, automata, and computational complexity. It seeks to understand the fundamental capabilities and limitations of computational systems and machines.
  1. Automata Theory:
  • Automata are abstract models that describe the behavior of computational systems. They can be used to analyze the capabilities of different machines and determine the types of languages they can recognize.
  • Finite Automata (FA), Pushdown Automata (PDA), and Turing Machines (TM) are common models studied in automata theory.
  2. Computability Theory:
     • Computability theory explores the boundaries of what can be computed. It investigates the notion of an effective method or algorithm and studies the concept of undecidability.
     • Turing's halting problem is a famous example of an undecidable problem.
  3. Complexity Theory:
     • Complexity theory focuses on the resources required to solve computational problems, such as time and space. It classifies problems based on their inherent difficulty and studies the relationship between different classes of problems.
     • Classes like P (polynomial time), NP (nondeterministic polynomial time), and NP-complete are central to complexity theory.
  • Difference between theory, lemma and coronary

  Theory	Lemma	Coronary
  A mathematical statement based on previously established statement	A minor result to prove another theorem	A result in which the proof relies heavily
  An example of a theory is Albert Einstein's general relativity theory, which describes the law of gravitation and its relationship to other natural forces.	..	..

• Proof by counterexample
  • Proof by counterexample is a method of mathematical or logical reasoning used to demonstrate that a given statement or conjecture is false. It involves providing a specific example that contradicts the statement being claimed, thus disproving its general validity.

• The Language of a DFA

  

• The Language of an NFA

  

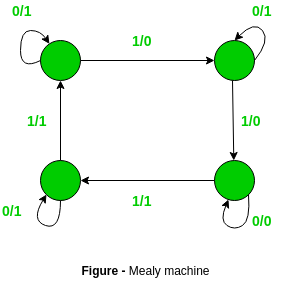
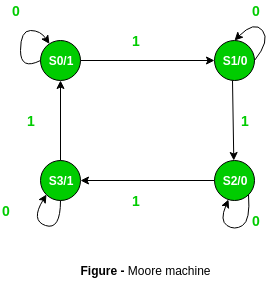
• Difference between more and mealy machine with example

• What do you mean by epsilon-closure ?
  • Epsilon closure refers to the set of all states that can be reached from a given state in a non-deterministic finite automaton (NFA) by following epsilon transitions (transitions that do not consume any input symbol).

• What are the uses of epsilon-transition?
  • Non-determinism: Epsilon-transitions are a key feature of non-deterministic finite automata (NFA). They allow the automaton to move from one state to another without consuming any input symbol.
  • Epsilon-closure: Epsilon-transitions are used to compute the epsilon-closure of a state in an NFA.
  • Conversion from NFA to DFA: Epsilon-transitions are utilized in the conversion process from an NFA to a deterministic finite automaton (DFA).
  • Regular expression construction: Epsilon-transitions are employed in constructing regular expressions from NFAs.
  • Language recognition and parsing: Epsilon-transitions play a role in determining whether a given string is accepted by an automaton or not.

• What is regular expression?
  • In the theory of computation, a regular expression is a formal notation that represents a regular language. It is an algebraic-like expression that describes a set of strings or a pattern of characters. Regular expressions are used to define and recognize regular languages in the context of formal language theory.

• The set of strings over alphabet {0, 1} that consists equal number of 0's and I's such that no prefix has two more 0's than 1's, nor two more I's than 0's.
  • (01+10)*

• The set of strings over alphabet (a, b, c) containing at least one a and at least one b.

  // ***a**b***  + ****b***a****
  
  R1 = (a+b+c)* a(a+b+c)* b(a+b+c)*
  
  R2 = (a+b+c)* b(a+b+c)* a(a+b+c)*
  
  RE for the given question R = R1+R2
  
  R = (a+b+c)* a(a+b+c)* b(a+b+c)* + (a+b+c)* b(a+b+c)* a(a+b+c)*

• Regular set of $(0+010)*$
  • $\{ \epsilon, 0, 010, 00, 0010, 010010, 01000, 00100100100, .... \}$
  • No two adjacent one

• Regular set of $(ab)*(bb)*b c$
  • $\{ bc, abbc, bbbc, abbbbc, ababbc, ababbbbc, ... \}$
  • No adjacent aa, cc, ac

• Define Arden's theorem.
  • If P and Q are two regular expressions over Ʃ and if P does not contain ε then the following equation in R given by R=Q+RP has a unique solution i.e., R=QP*.

• Show the RE for the following DFA using state-elimination technique:

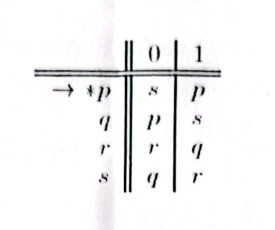
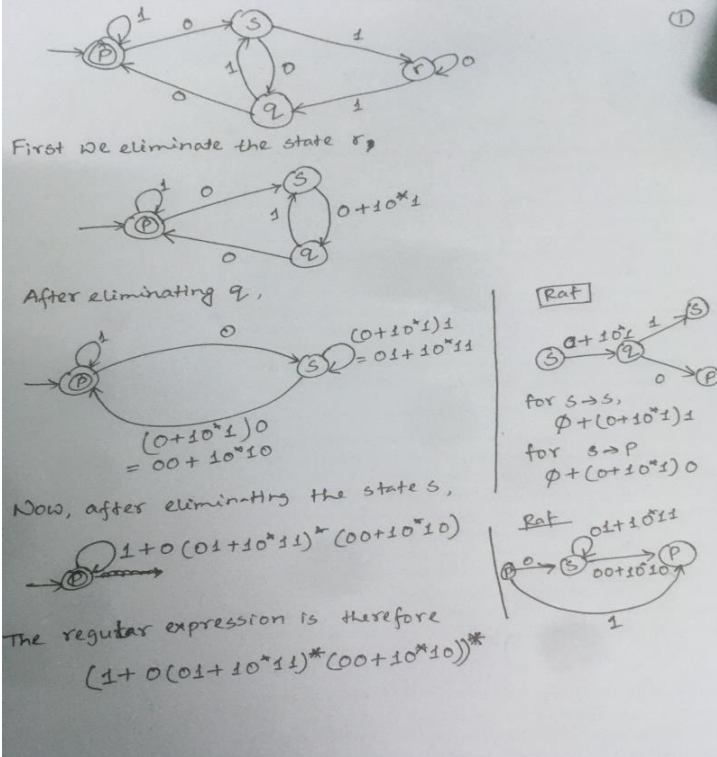
Using Arden’s theorem:

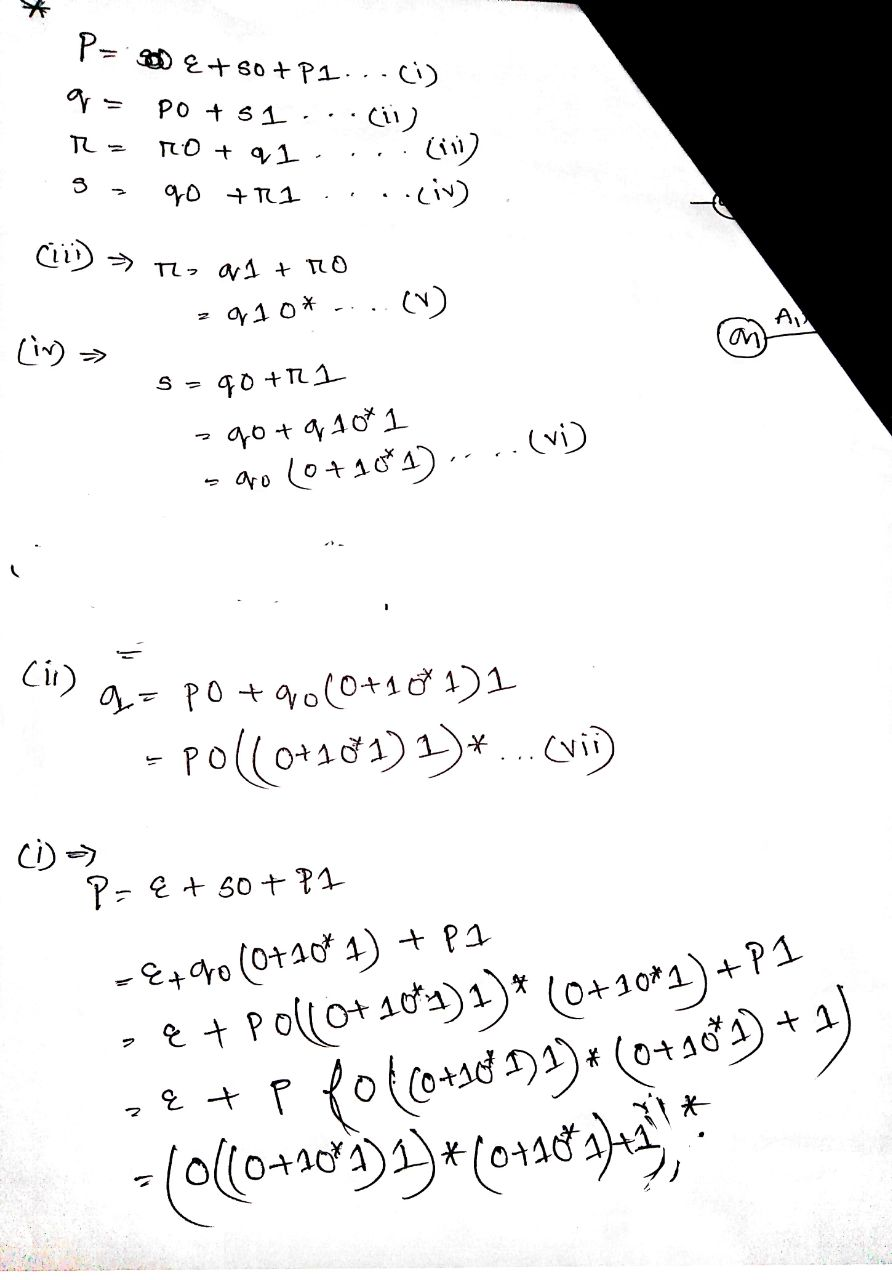
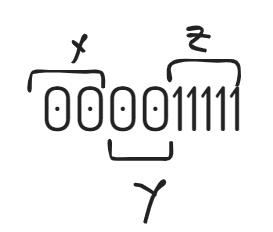
• Why pumping lemma is required? Write down the properties of pumping lemma.
  • The pumping lemma is a tool used in formal language theory to prove a language not a regular.
  • For any regular language L, there exists an integer P, such that for all w in L

    |w|>=P

    We can break w into three strings, w=xyz such that.

    (1)lxyl < P

    (2)lyl > 1

    (3)for all k>= 0: the string $xy^kz$ is also in L

• Differentiate between ambiguity and inherent ambiguity with examples

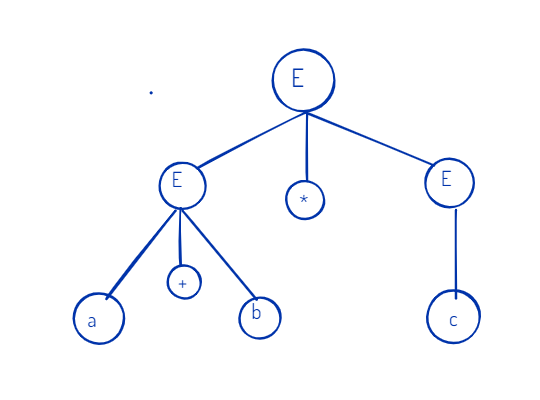
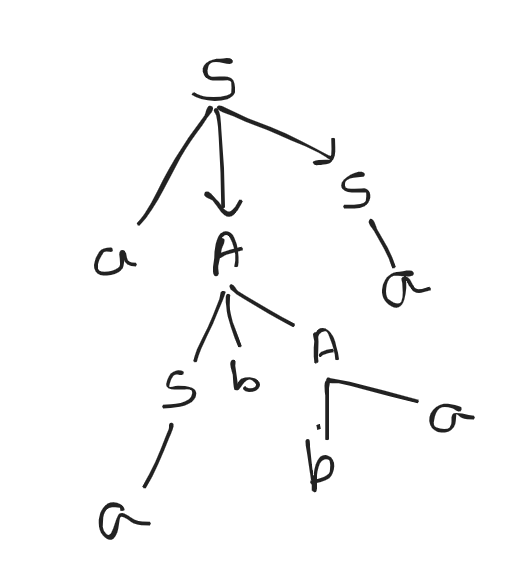
• Consider the following grammar and show a derivation tree for the string a + b * c:

  $E= E+E |E*E|a|b|c$

  • Derivation tree is a graphical representation for the derivation of the given production rules for a given CFG

• Then prove that the grammar is an ambiguous grammar
  • Because there is an another derivation tree

    

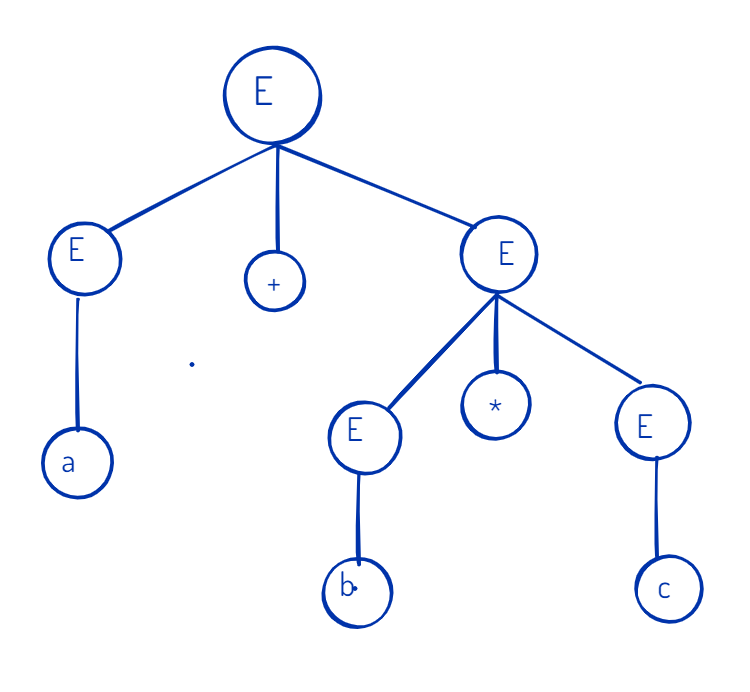
• Show how to eliminate ambiguity from the grammar.
  • We can use Precedence and Associativity to remove the ambiguity from some grammar.

    How

    $E$ = First level of Precedence

    $T =$ Second level of Precedence

    $F =$ Generating Basic Units/Terminal

    • Simply make the grammar Left Recursive by replacing the left most non-terminal
      • $E = E + T | T$
    • The unambiguous grammar will contain the productions having the highest priority operator (“*” in the example) at the lower level and vice versa. The associativity of both the operators are Left to Right.

      $$E =E+T | T \\ T = T * F | F \\ F= a|b|c$$

• Write down the language of a Pushdown Automata (PDA).

  

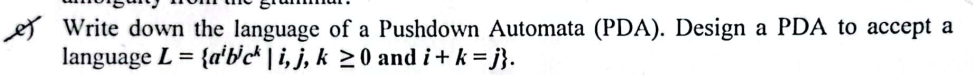
1. Since S is in right side we have to add S' -> S :

   $$S' -> S \\ S-> bA | aB \\ A-> bAA | aS | a \\B-> ABB | bS | b$$

2. Removing Null Pointer : There's no null pointer

3. Remove Unit Production:
   After removing S' -> S :
   

4. Removing Useless symbol

4. Replacing the productions that has more than two variables in RHS
   

5. Change in Production where terminal is left of variable where P → qA

• What is Turing machine ? Describe formal notation of Turing machine?
  • A Turing machine is an computational model like FA, PDA which works on unrestricted grammar.

    Formal Notations:

    $M = \{ Q, X, \Sigma, \delta, q{_0}, B, F\}$

    Q = Non-empty set of states

    X = set of tape Alphabets

    $\Sigma$ = Input states

    $\delta$ = Transition function $Q * X -> Q * X * \{ Left Shigt, RightShift \}$

    $q{_0}$ = Starting state

    B = Blank Symbol

    F = Final State

• Fermat’s Last Theorem
  • Fermat's last theorem, also called Fermat's great theorem, the statement that there are no natural numbers (1, 2, 3,…) x, y, and z such that $x^n + y^n = z^n$ , in which $n$ is a natural number greater than 2.

• Fermat’s Little Theorem states that if p is a prime number, then for any integer a, the number a p – a is an integer multiple of p.

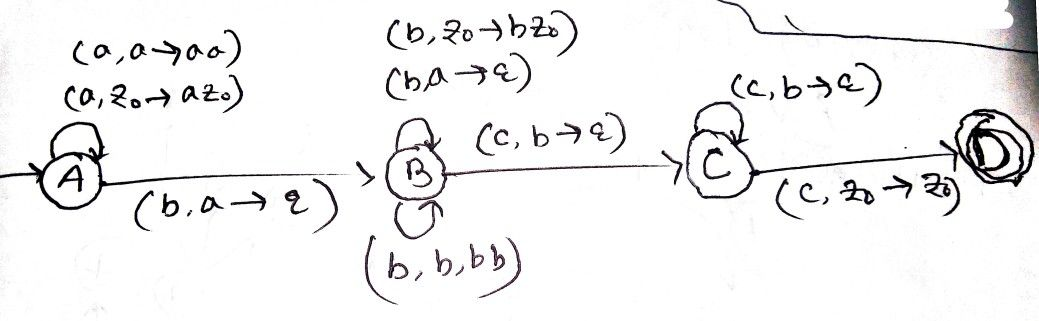
• Design a Turing machine that takes a input as Number and adds 1’s to it binary.

  

  • Partial Recursive Function
    • A function which is not defined for some inputs of the right type, that is, for some of a domain. For instance, division is a partial function since division by 0 is undefined (on the Reals).
    • A partial function is called partial recursive if it can be computed by a Turing machine; that is, if there exists a Turing machine that accepts input x exactly when f(x) is defined, in which case it leaves the string f(x) on its tape upon acceptance.

      By Church's thesis, a function is recursive if and only if it is computable.

• Define extended transition function.
  • An extended transition function $\hat\delta$ traces the path of an automaton and determines the final state when an initial state q and an input string x are passed through it.

    Steps of the recursive algorithm to solve

    1. Base Condition

       $\hat\delta(q, \epsilon) = q$

    2. Recursive Solution

       $\hat\delta (q, xa) = \delta (\hat\delta(q, x), a)$

• Process NFA using extended transition function

  

• Describe briefly about the operators of regular expression
  • Union: If R1 and R2 are regular expression then R1 | R2 (R1 U R2 or R1 + R2) is also.
    • L(R1|R2) = L(R1) U L(R2).
  • Concatenation: If R1 and R2 are regular expression then R1R2 is also.
    • L(R1R2) = L(R1) concatenated with L(R2).
  • Kleene closure : If R1 is regular expression then R1* is also.
    • L(R1*) = epsilon U L(R1) U L(R1R1) U L(R1R1R1) U ...

Closure has the highest precedence, followed by concatenation, followed by union.

• When a symbol is useful for a grammar ? Explain.

  A symbol can be useful if it appears on the right-hand side of the production rule and takes part in the derivation of any string/reachable from start

  T → aaB | abA | aaT  
  A → aA  
  B → ab | b  
  C → ad
  
  Where T,A,B is useful but C not.

• $\epsilon-NFA$ to $DFA$

  

• How to draw a Parse tree. Explain.
  • A parse tree is a graphical representation of how the symbols in a sentence can be derived from the non-terminal symbols of a grammar
  • Steps:
    • Start with the start symbol as root
    • Apply Production rule from the root
    • Continue expanding production rule recursively until all leaf nodes are terminals
    • Finalize the parse tree

  Example:
  S -> sAB
  A -> a
  B -> b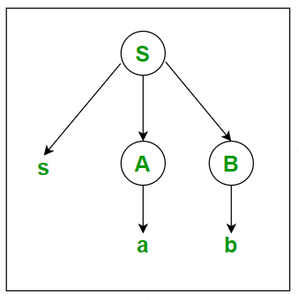

  

• Rijk Method

• K==0

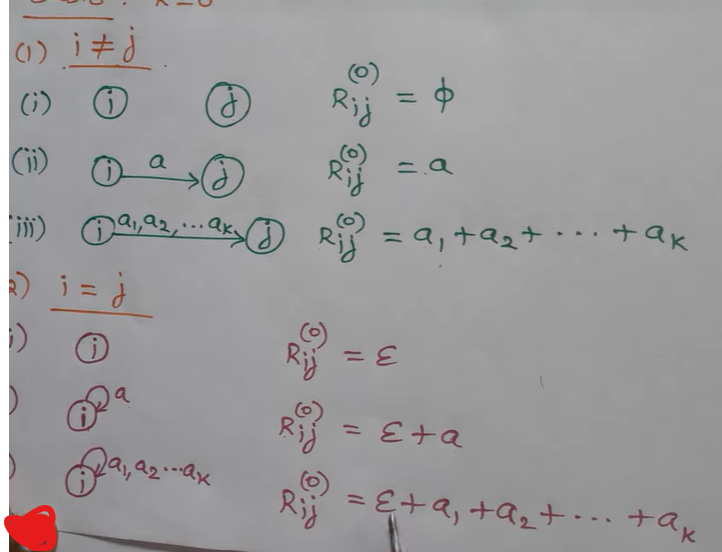
• K ≠ 0

$R{_i}{_j}^k = R{_i}{_j}^{k-1} + R{_i}{_k} (R{_k}{_k}^{k-1})^* R{_k}{_j}^{k-1}$

• Define language in automata with example
  • A language is a subset of $\Sigma^*$ for some alphabet $\Sigma$ .
  • Example : The possible language for length 2, $\Sigma = \{ a, b \} \\ L = \{aa, ab, ba, bb, ..\}$

• Prove that, $L = \{0^n10^n | n \gt 0 \}$ is not a regular language.

  Concept:

  • Pumping lemma is used to prove a language not regular.
    • Theorem : If A is a regular language has a pumping length ‘P’ such that any string S where $|S| \geq P$ maybe divided into three parts $S = xyz$ that the following condition must be true
      • $|xy| \leq P$
      • $|y| \gt 0$
      • $xy^iz \space \epsilon \space A$, for every $i > 0$

    Prove:

    Suppose that, $L$ is a regular language.

    Pumping length is 4.

    $w = 000011111$

    Case 1:

    • $y$ has only 0’s

      

    $|xy| \leq 4$

    $|y| > 0$

    $xy^2z = 00000011111$ $\not\epsilon$ $A$

    Case 2:

    • $y$ has only 1’s

    …

    Case 3:

    • $y$ has 01

    …

• What are the strategies for constructing a regular expression from a finite automation using state-elimination method. Explain

  Steps:

  • If there exists any incoming edge to the initial state, then create a new initial state having no incoming edge to it
  • If there exists multiple final states in the DFA, then convert all the final states into non-final states and create a new single final state
  • If there exists any outgoing edge from the final state, then create a new final state having no outgoing edge

  

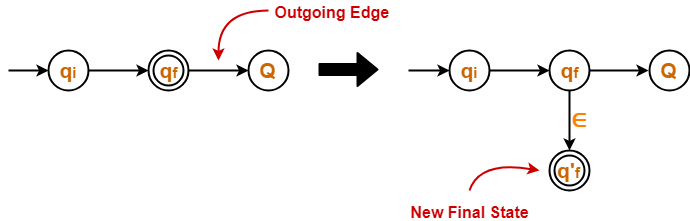
  • After following the above rules we can eliminate all intermediate state one by one.

• Describe formal notation of pushdown automata.

  Pushdown Automata is a finite automata with extra memory called stack which helps Pushdown automata to recognize Context Free Languages.

  A PDA can be formally described by 7-tuples.

  $\{ Q, \Sigma, \tau, \delta, q_0, Z_0, F \}$

  $Q$ : Non-empty set of states

  $\Sigma$ : Nonempty set of input symbols

  $\tau$ : Nonempty set of pushdown symbols

  $\delta$ : Transition function $Q x \{Σ ∪ ∈\} x Γ \rarr Q x Γ*$

  $q_0$ : Initial State

  $Z_0$ : Initial Symbol on the pushdown store/stack

  $F :$ Final State

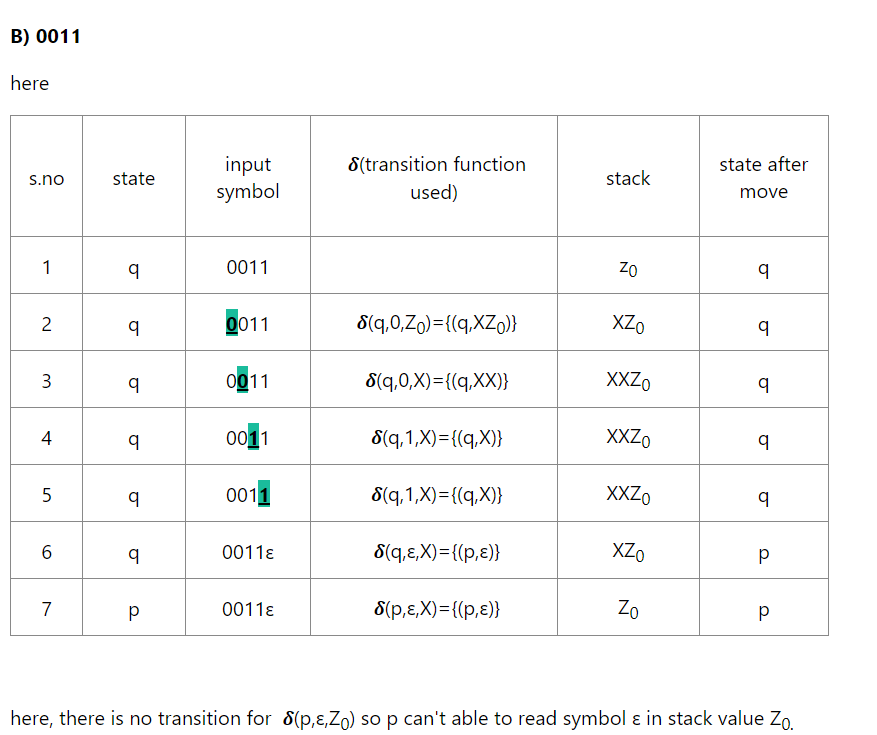
• Design a PDA language to accept a language $L = \{a^ib^jc^k | i,j,k \geq0 \space and \space i=j \space or \space j=k \}$

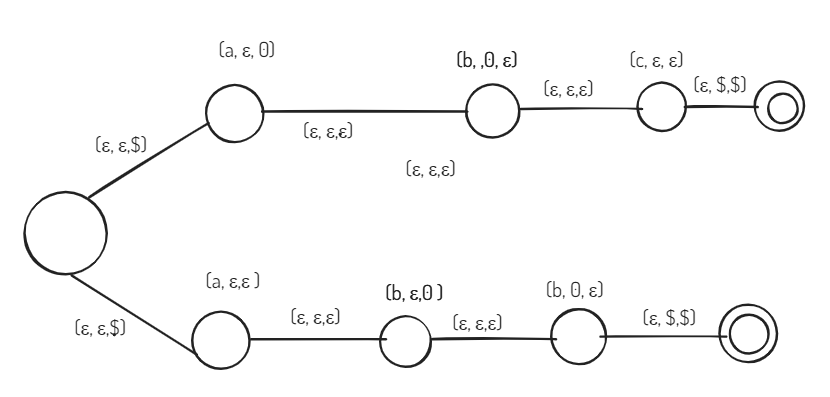
The transitions on state are self-loop

• Define Chomsky Normal Form(CNF)

A grammar where every production is either of the form A → BC or A → c (where A, B, C are arbitrary variables and c an arbitrary symbol).

A CFG is in CNF if all production rules satisfy following conditions

• Start symbol symbol generating ε $A \rarr \epsilon$

• A non-terminal generating at most two non-terminals $S \rarr AB$

• A non terminal generating a terminal $A \rarr a$

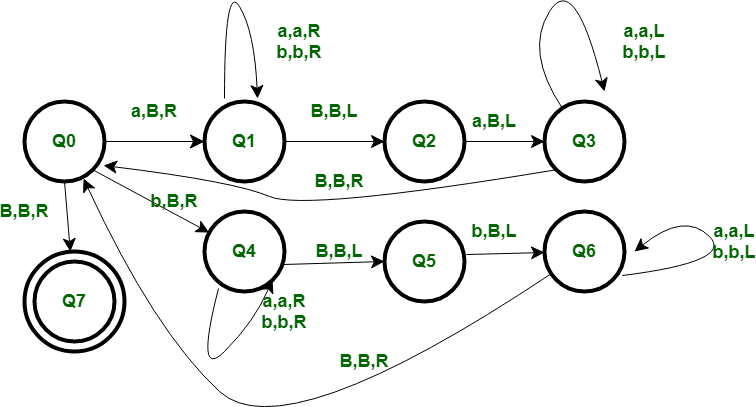
• What is transition Diagram ?

  Transition diagram can be interpreted as a flowchart for an algorithm recognizing a language.

  Which is constructed by

  • There is a node for each state in Q, represented by the circle
  • There is a directed edge from a node p to node q labeled if $\delta (p, a) = p$
  • Starting state, there is an arrow with no source
  • Final states indicating by a double circle

• Write down the application of Context Free Grammar
  • Context Free Grammar is a formal grammar which is used to generate all possible strings in a given formal language.
  • Applications:
    • Used in compilers (Such GCC) parsing
    • define the syntax of programming languages
    • Used to define the high level structure of a programming language
    • Natural Language Processing (NLP)

• Draw a PDA for the language $L_{wwr} = \{WW^R | W \space is \space in \space (0+1)^* \}$

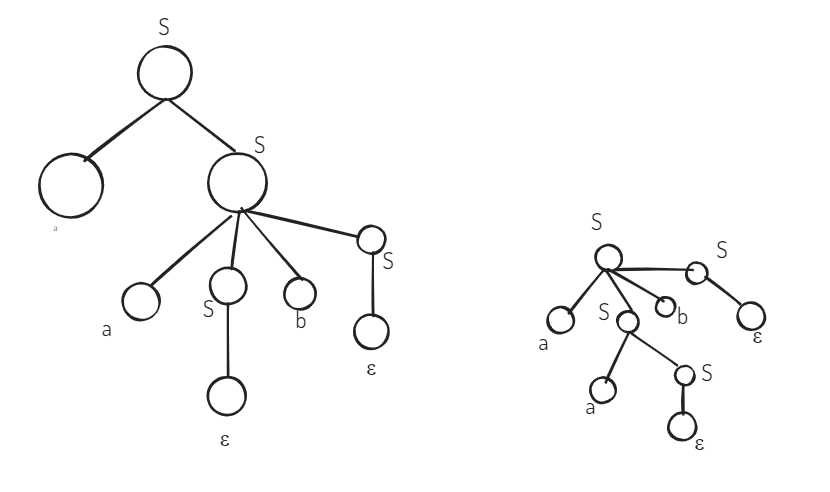
• Define the language of a grammar

  Language of a grammar is the set of all strings that can be generated by that grammar.

$(i)$

Useful symbols $= \{a, b, A, B, S, D\}$

$C$ is Useless.

Grammar :

$S \rarr aAa | bBb |\epsilon \\ A \rarr a \\ B \rarr b \\ D \rarr A | B |ab$

$(ii)$

Eliminating $S \rarr \epsilon$ :

$(iii)$

Eliminating $D \rarr A$ & $D \rarr B$ (Unit Production):

$S \rarr aAa | bBb \\ A \rarr a \\ B \rarr b \\ D \rarr a | b |ab$

$(i)$ Leftmost Derivation

S → $aAS$

$(ii)$ Rightmost Derivation

$S \rarr aAS$

$(iii)$ Parse tree

$(i)$

Leftmost derivation

$E \rarr E * E$

$II*E$

$aI*E$

$aI*(E)$

$aI * (E+E)$

$aI * (II+E)$

$aI*(IbI+E)$

$aI*(abI + E)$

$aI*(abI +I0)$

$aI*(abI +II0)$

$aI*(abI +bI0)$

$aI*(abI +bIa0)$

Rightmost derivation

$E \rarr E*E$

$E*(E)$

$E * (E+E)$

$E*(E+I)$

$E*(E+II)$

$E*(E+bI)$

$E*(I+bI)$

$E*(I0+bI)$

$E*(a0+bI)$

$I*(a0+bI)$

$I0*(a0+bI)$

$II0*(a0+bI)$

$IIa0*(a0+bI)$

$bIa0*(a0+bI)$

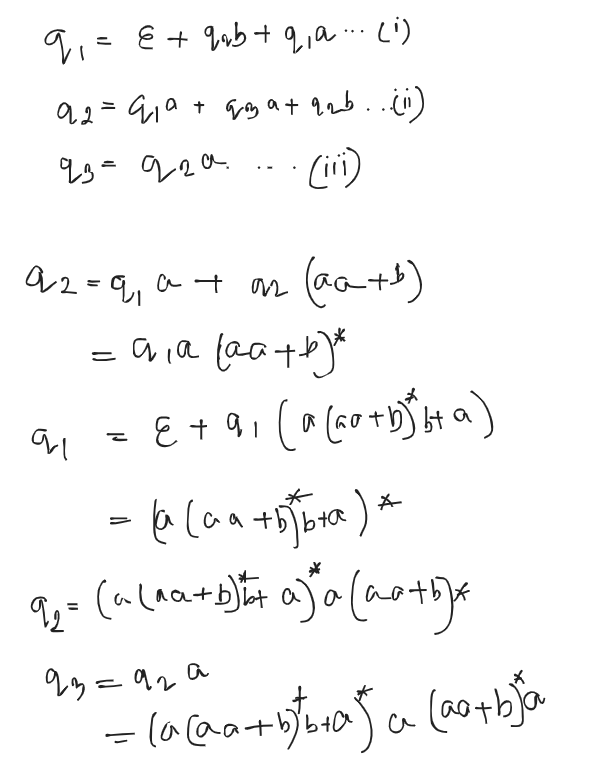
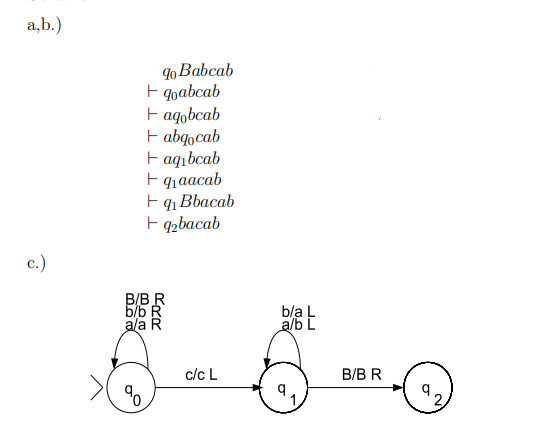
• Instantaneous Description (ID)

  Instantaneous Description (ID) is an informal notation of how a PDA “computes” a input string and make a decision that string is accepted or rejected.

Type of Complexity Classes

• P : that can be solved by a deterministic machine in polynomial time.

• NP: can be solved by a non-deterministic machine in polynomial time

• NP-hard: An NP-hard problem is at least as hard as the hardest problem in NP and it is a class of problems such that every problem in NP reduces to NP-hard.

• NP-Complete: A problem is NP-complete if it is both NP and NP-hard.