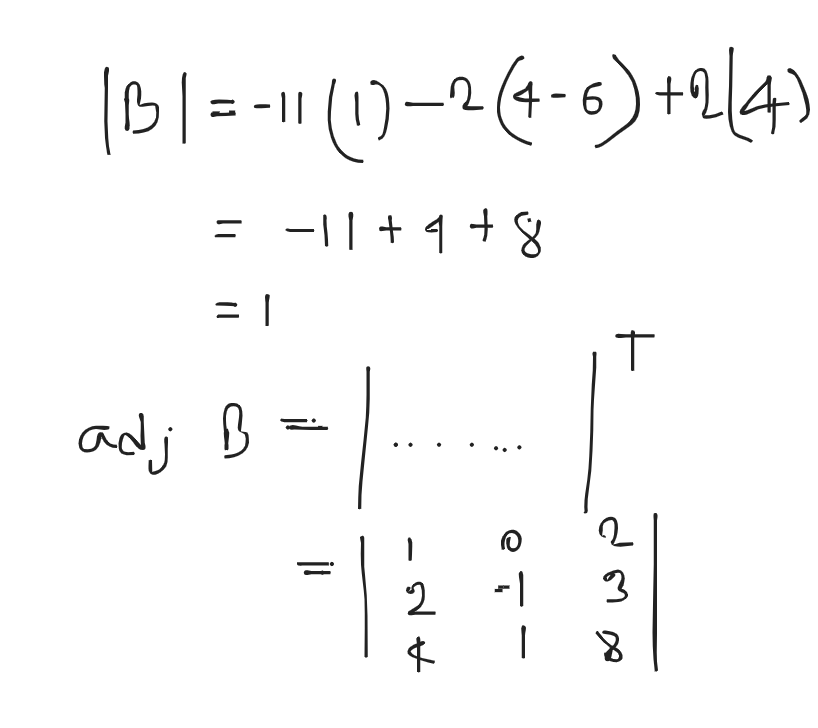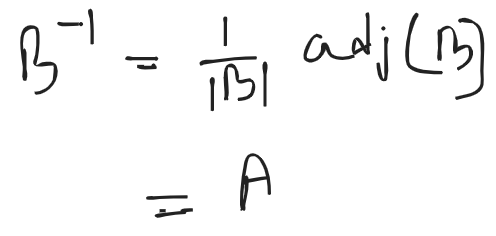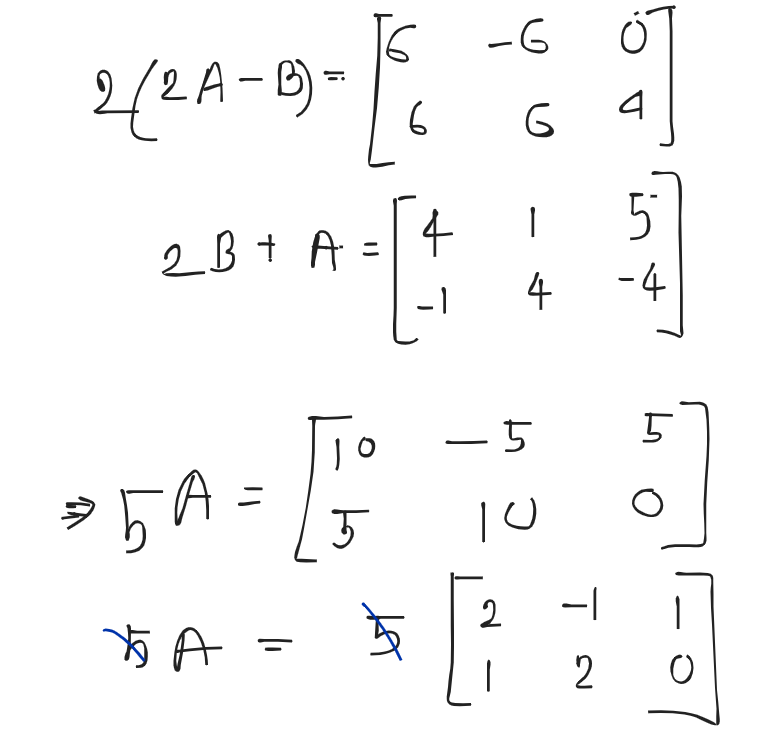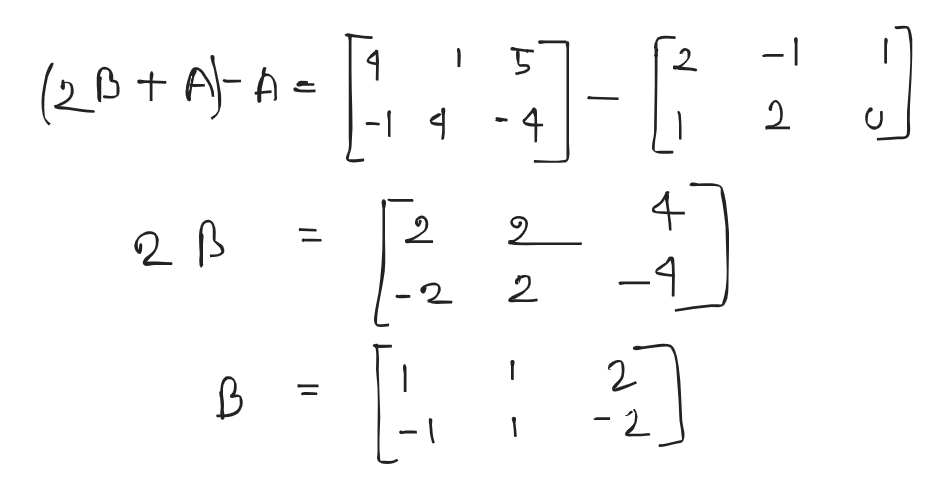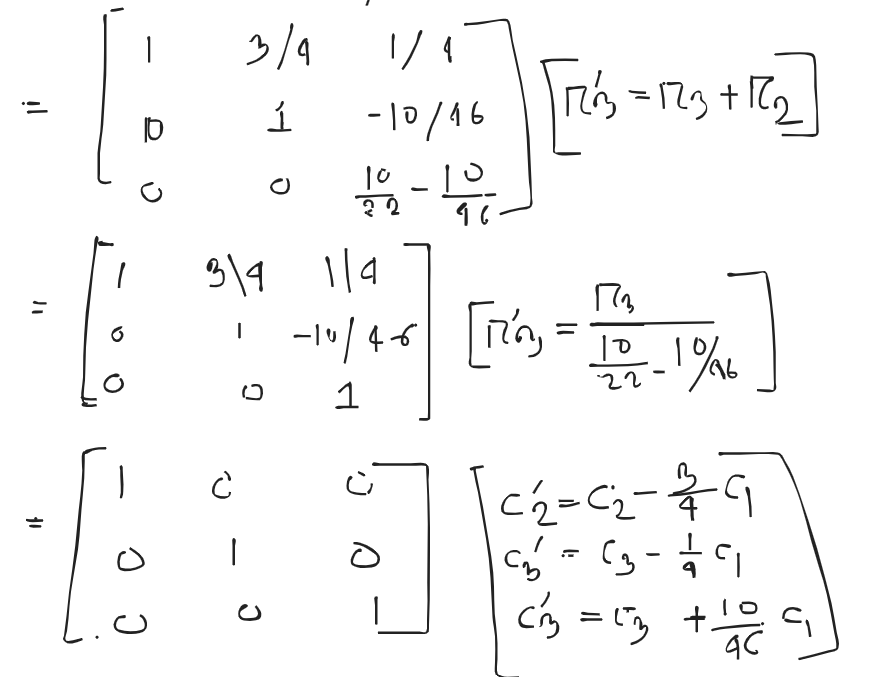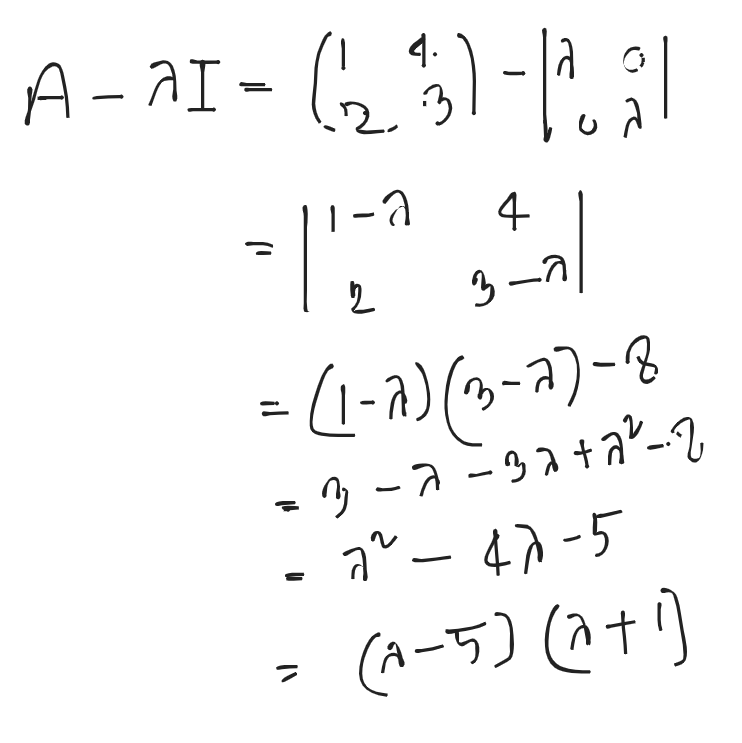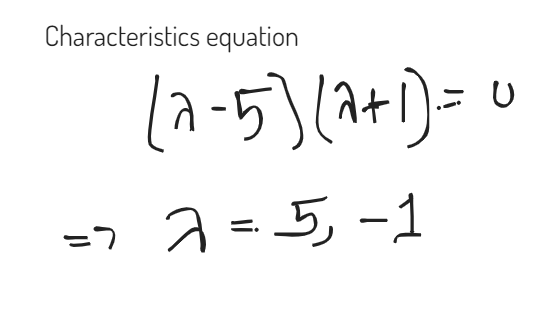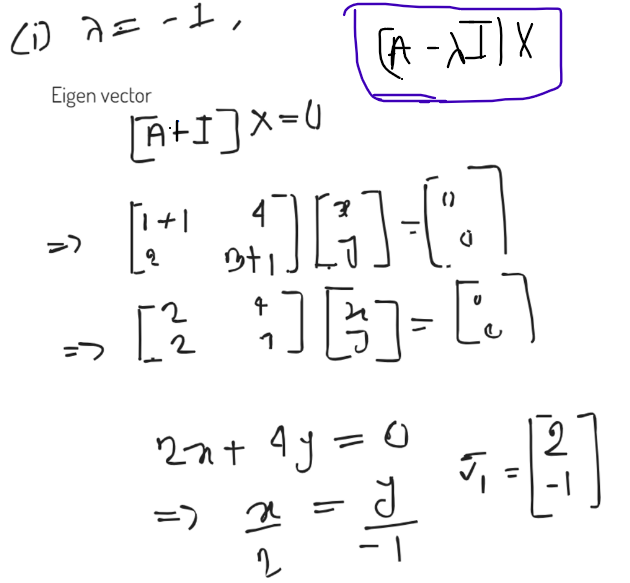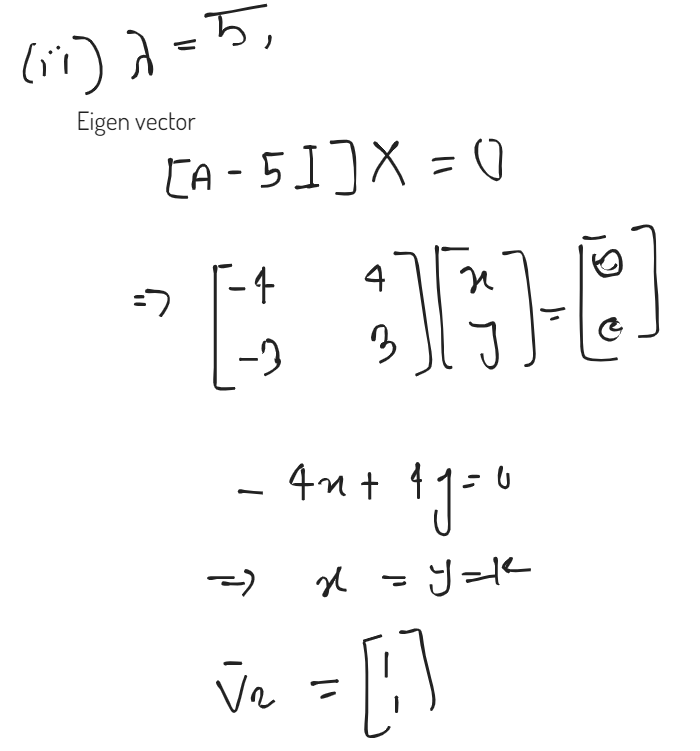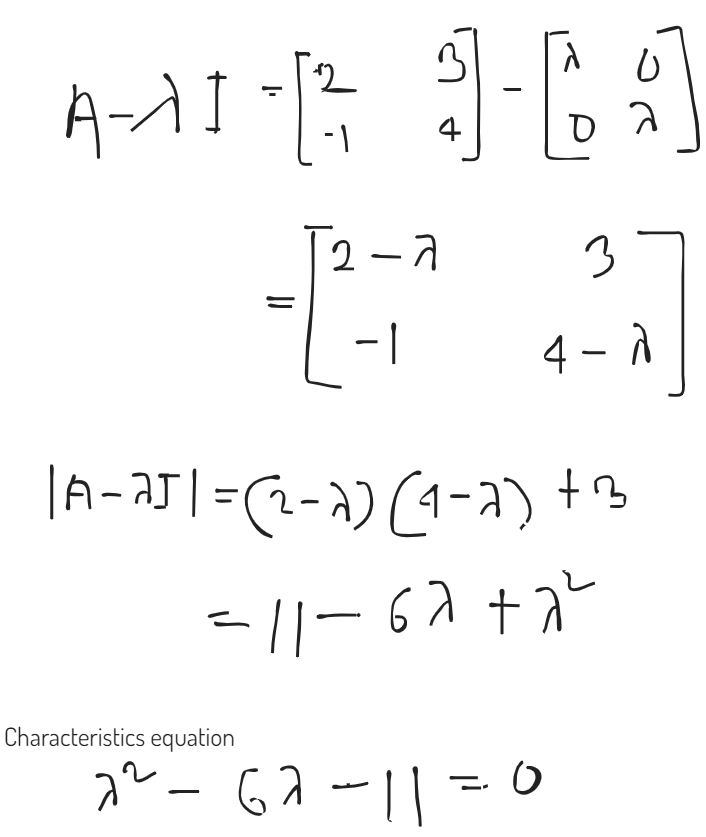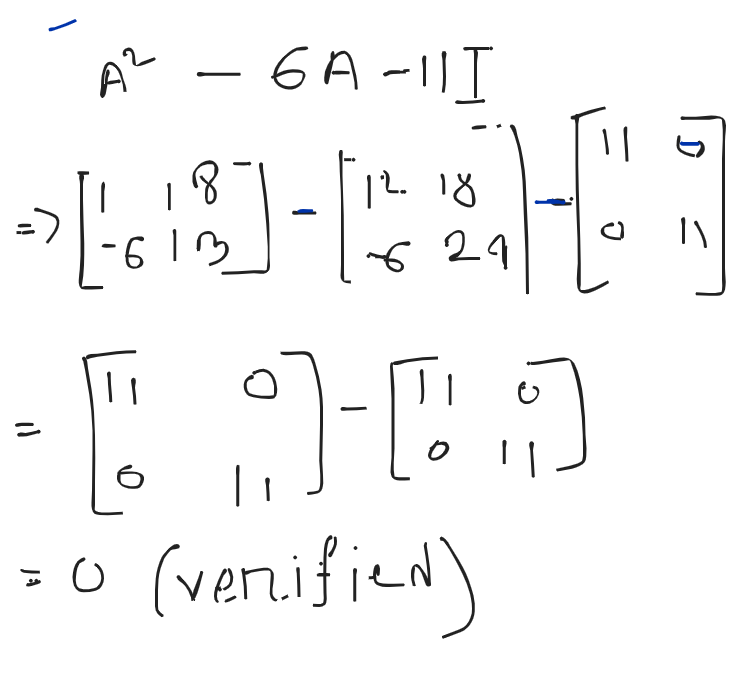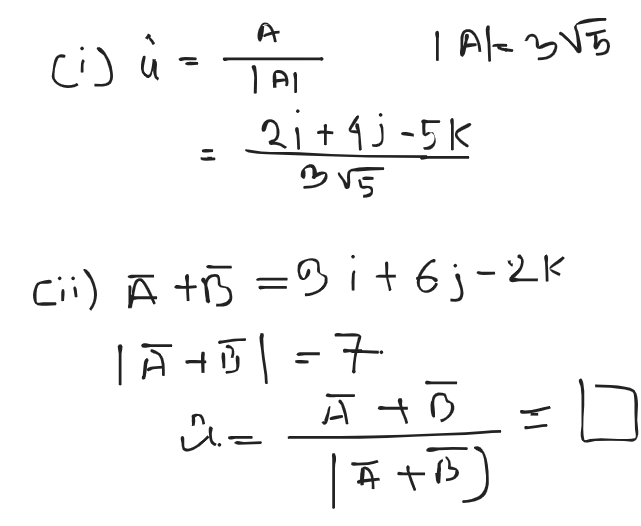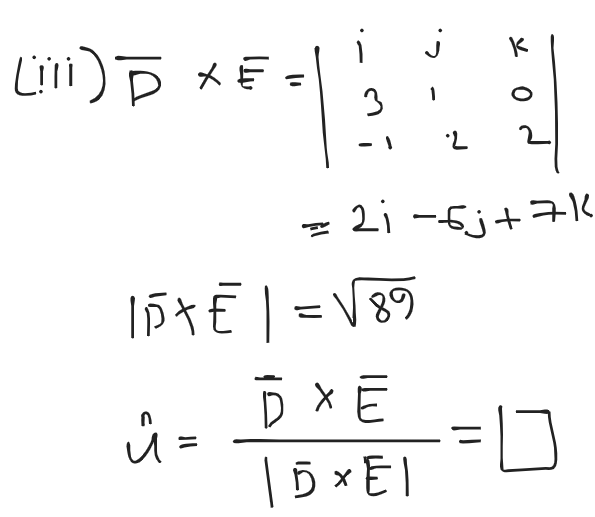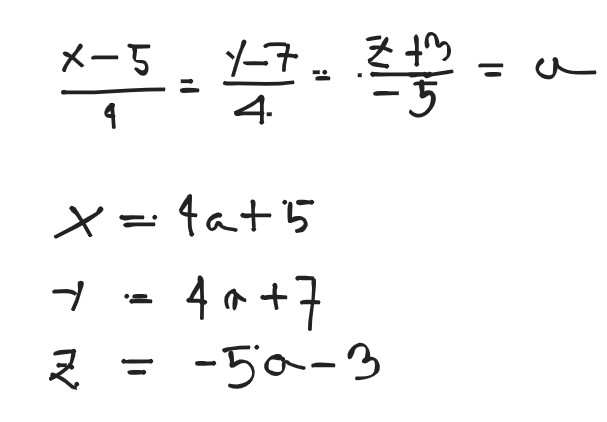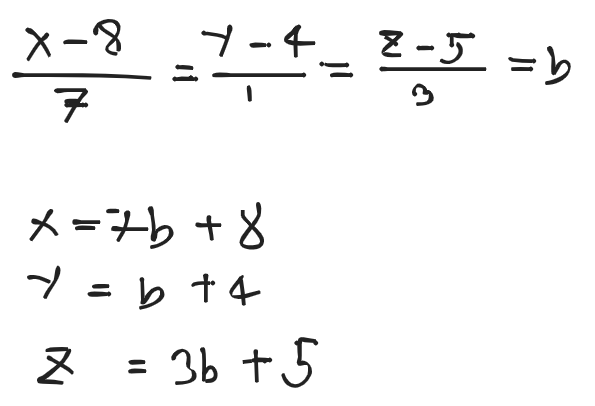Matrices, Vector Analysis and Co-ordinate Geometry

Created by	BBorhan
Last edited time	@October 14, 2023 12:20 PM
Tag

Define diagonal matrix, Scalar matrix, Hermitian matrix, Idempotent matrix and nil
potent matrix

Ans:

Diagonal Matrix : A square matrix in which every element except principle diagonal is zero.

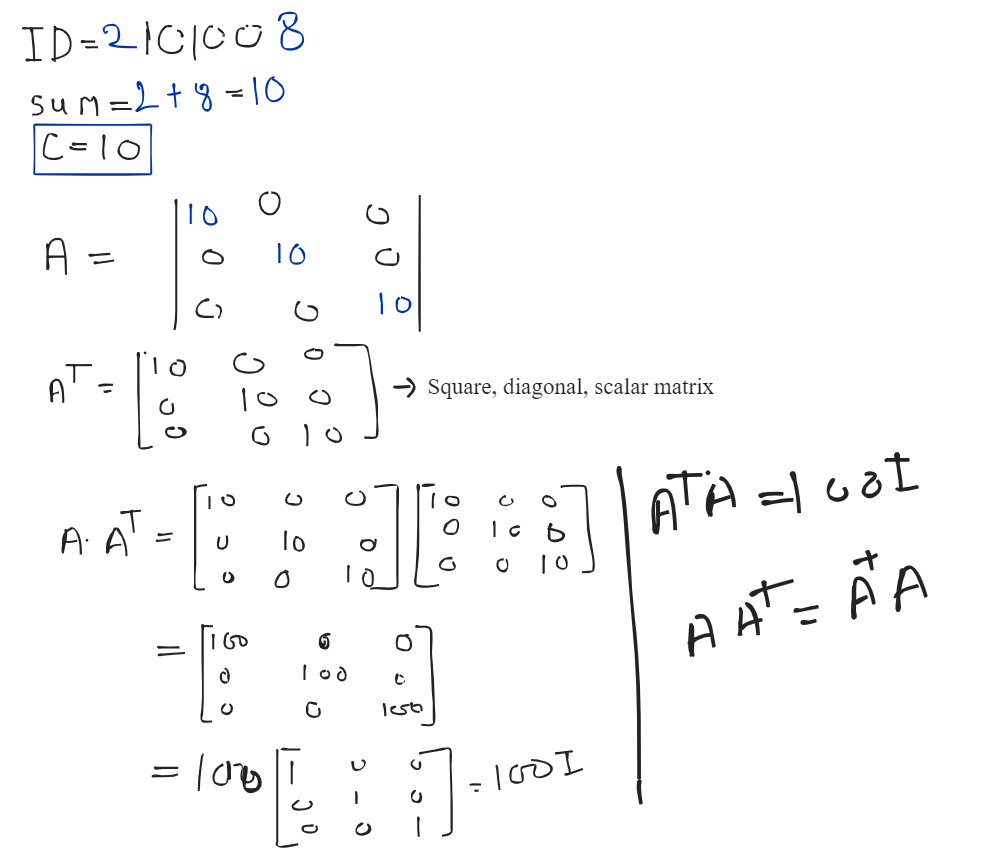
Scalar Matrix : A type of diagonal matrix in which all diagonal element are same.

Hermitian matrix: A complex square matrix that is equal to its own conjugate transpose matrix.

Idempotent matrix: An idempotent matrix is one that when it multiplied by itself produces the same matrix.

Nilpotent matrix : A type of square matrix which produces a null matrix when it is multiplied by itself.

Define diagonal and tri-diagonal matrix with examples.

Ans:

Diagonal matrix: A square matrix in which every element except principle diagonal is zero.

Tri-diagonal matrix: A square matrix in which every element except the major three diagonal is zero.

Ans:

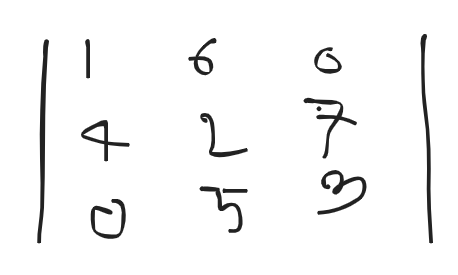
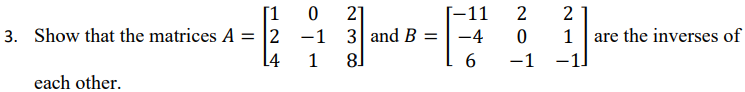
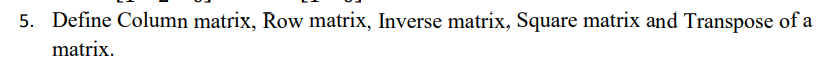
Ans:

Column matrix : A matrix having only 1 column

Row matrix : A matrix having only one row

Inverse matrix: If $A$ is a non-singular matrix, there existence of $n * n$ matrix $A^-1$ which is called the inverse matrix of $A$ such that it satisfies the property

$AA^{-1} = I$ , where $I$ is an identity matrix

Square matrix: A matrix having same number of rows and columns

Transpose of a matrix : The transpose of a matrix can be defined as an operator which can switch the rows and column indices of a matrix.

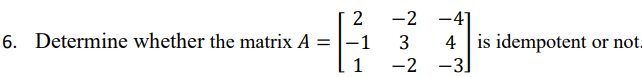
Ans:

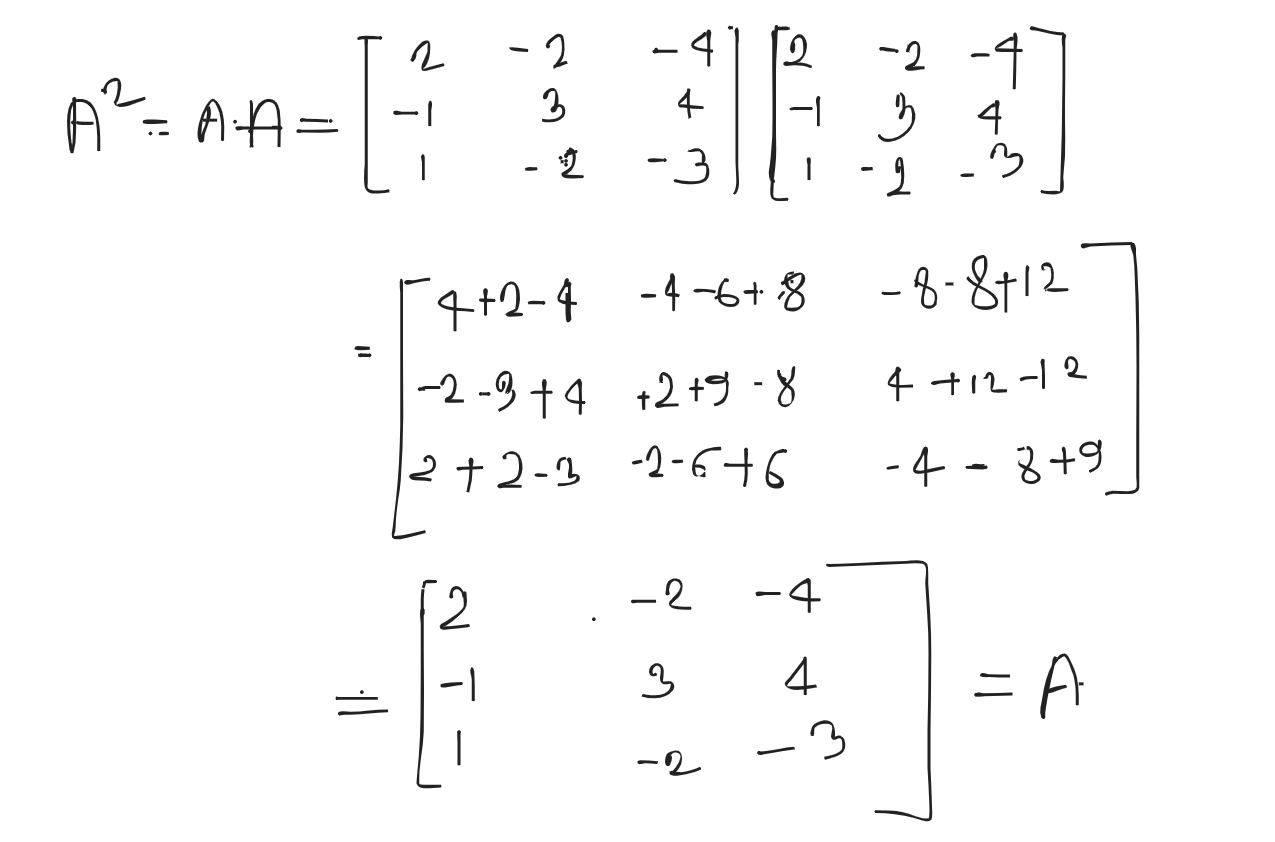
Hence, it’s an idempotent matrix.

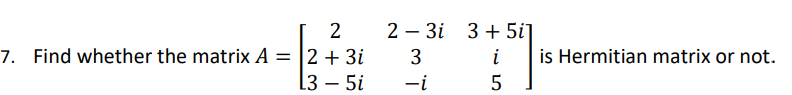
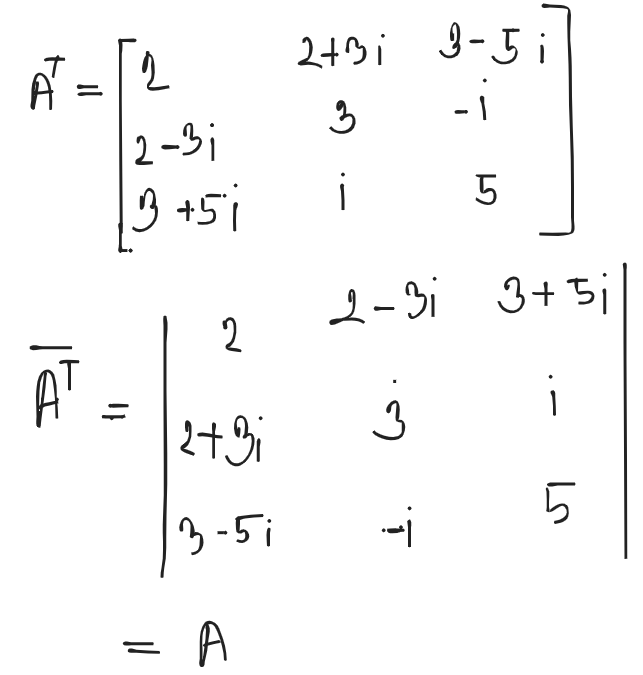
So, it’s Hermitian matrix

💡

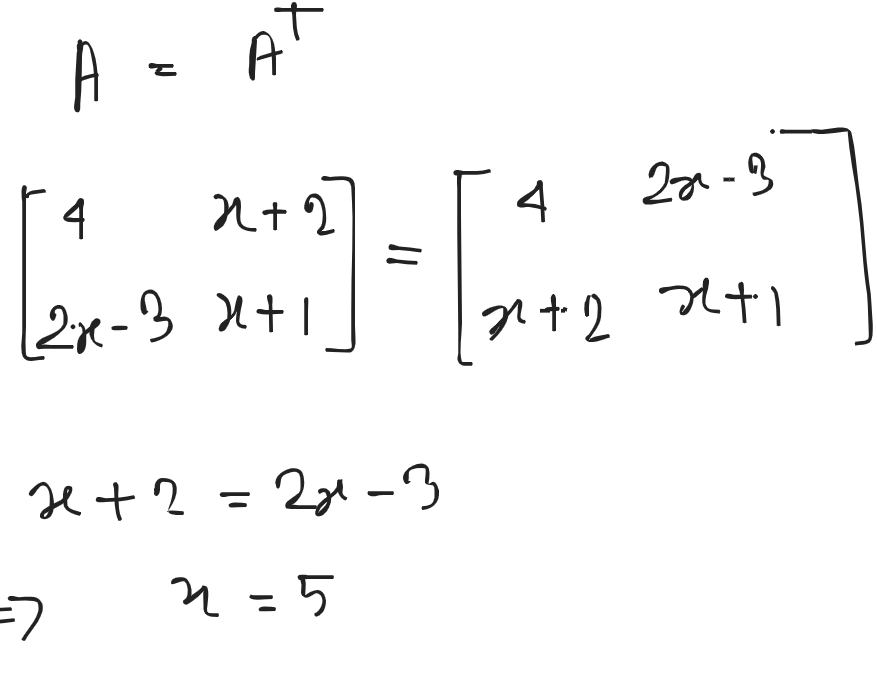
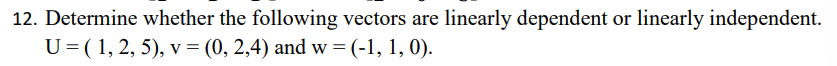
determinant ≠ 0 → Linearly independent

determinant = 0 → Linearly dependent

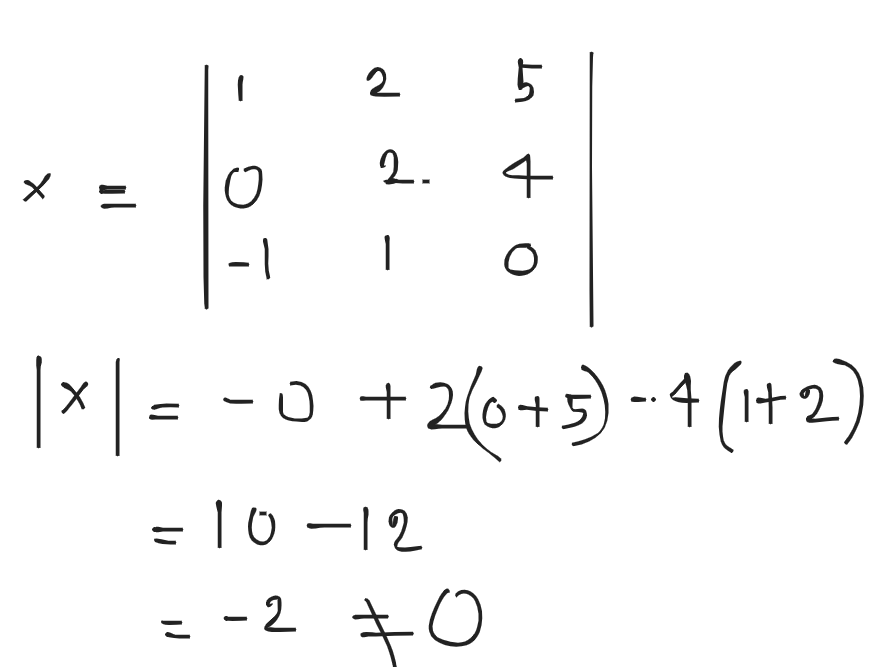
Hence, it is linearly independent.

💡

No Solutions:

For this to occur we must have a row where the left side is all zeros, but the right side is not

[0 0 0 | z]

Infinitely Many Solutions/More than one solution:

This occurs when we have a free variable. This is achieved by getting a whole row (including the right side) or column to be zeros:

[0 0 0 | 0]

Unique

We must have a leading term for each column.

$(i)$ $a=-3$

$(ii)$ $a=2$

$(iii) a \not= -3,2$

💡

Rank of a Matrix
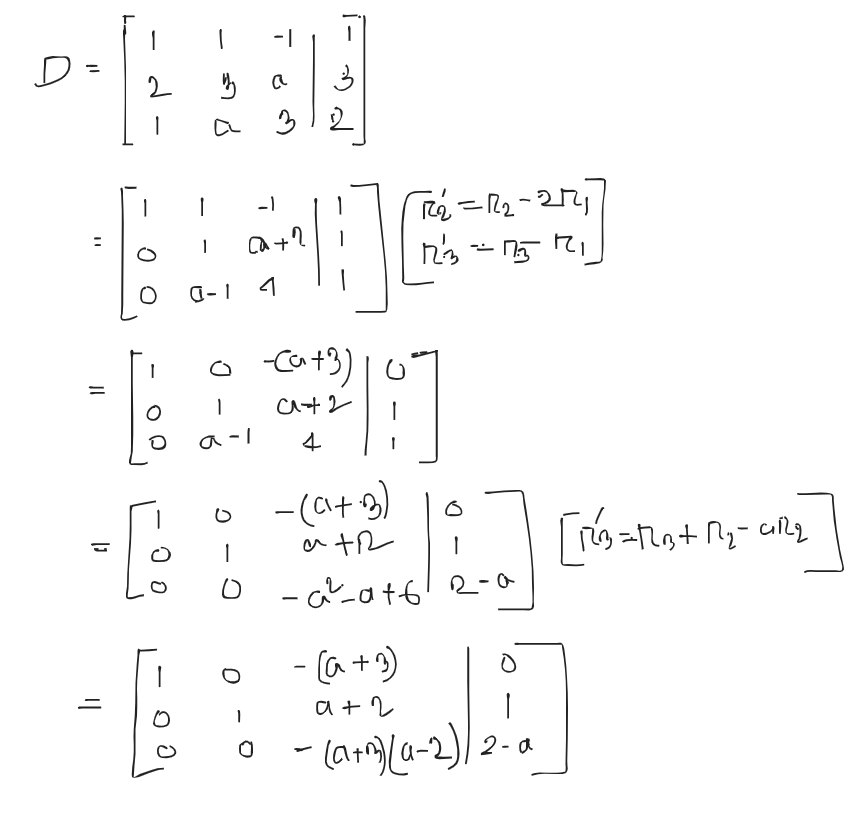
The maximum number of linearly independent rows of a matrix is called the rank of a matrix.

Find the Row Echelon, count the number of non-zero row(s).

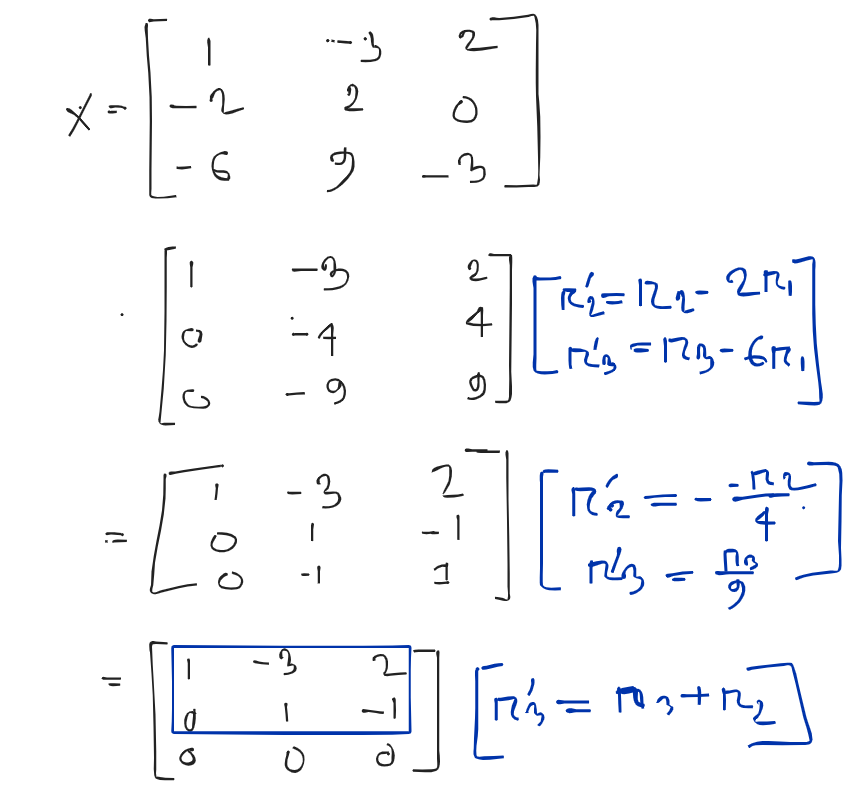
The rank of the matrix is $2$ .

Rank of a matrix: The number of linearly independent rows in a matrix

The rank of the matrix 3.

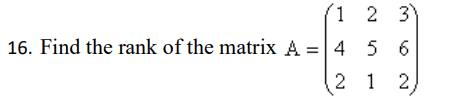
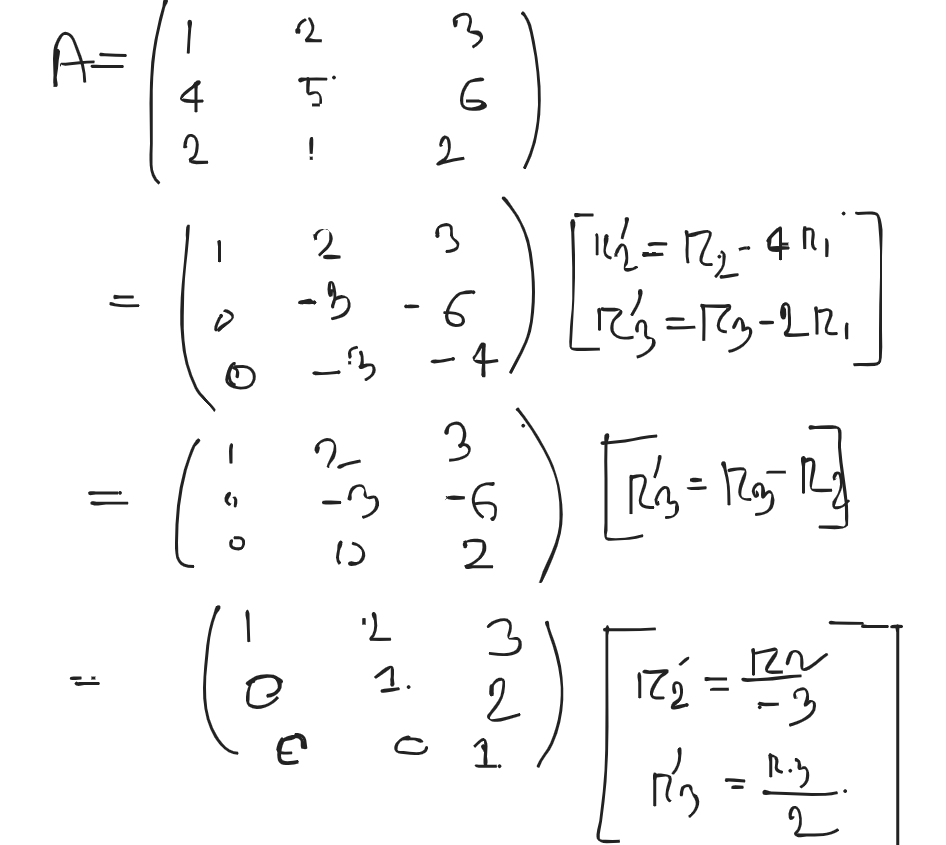
The rank of the matrix is 3.

$(i)$

$(ii)$

$(iii)$

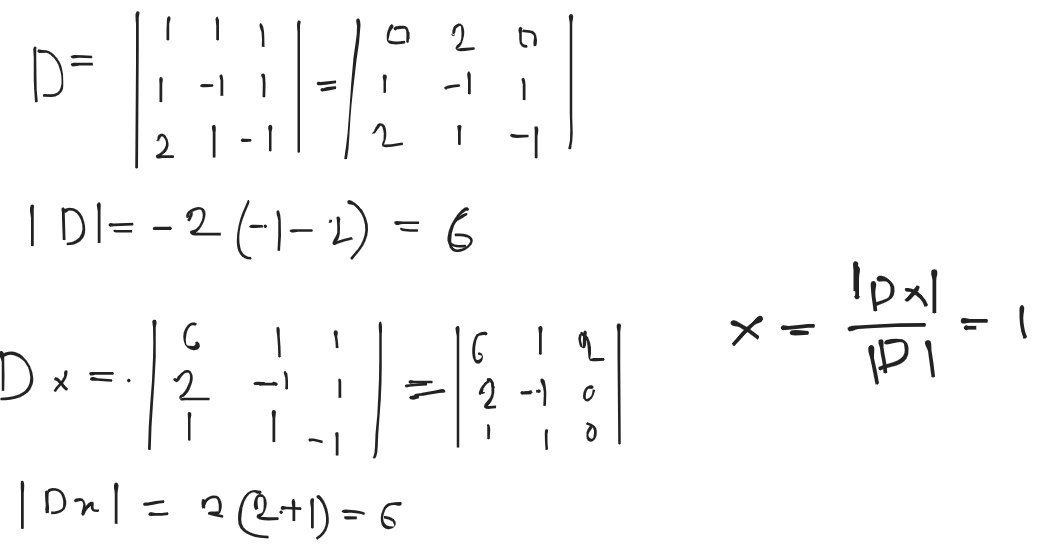
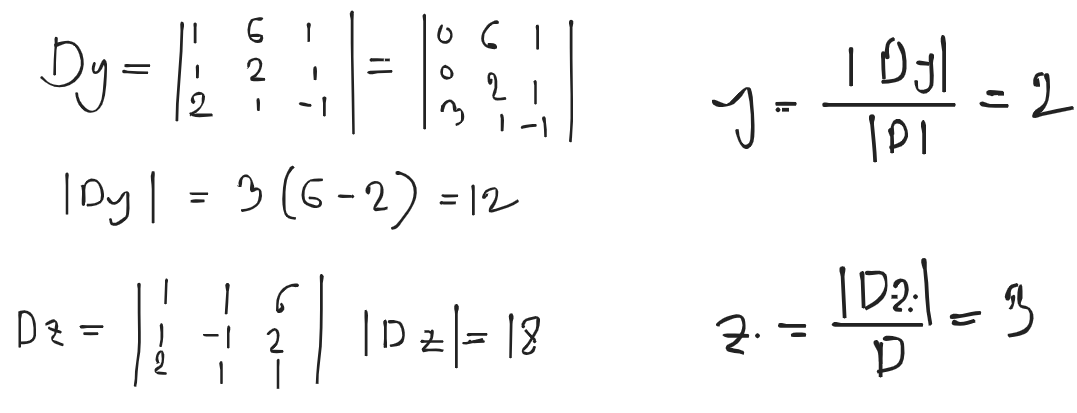
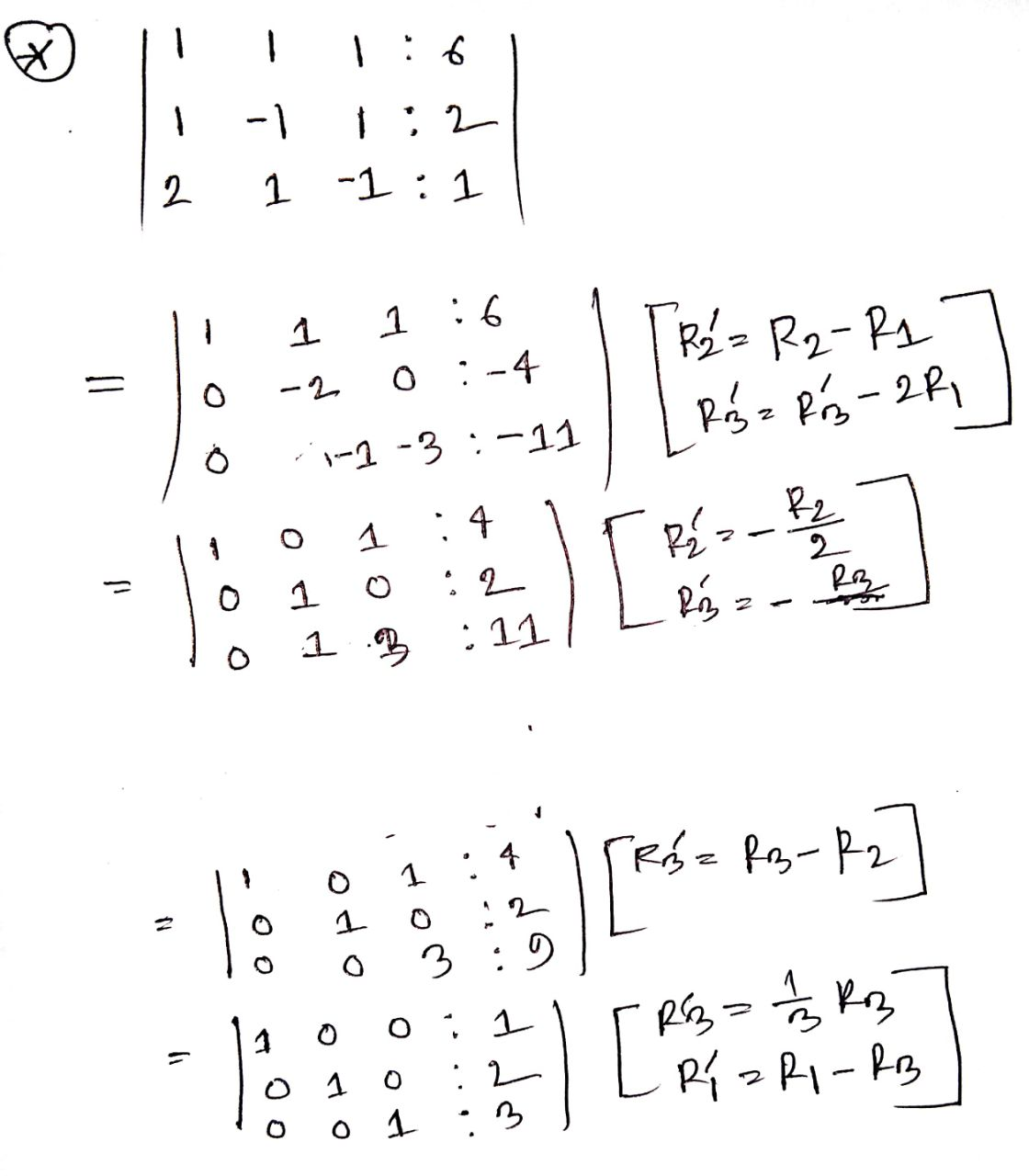
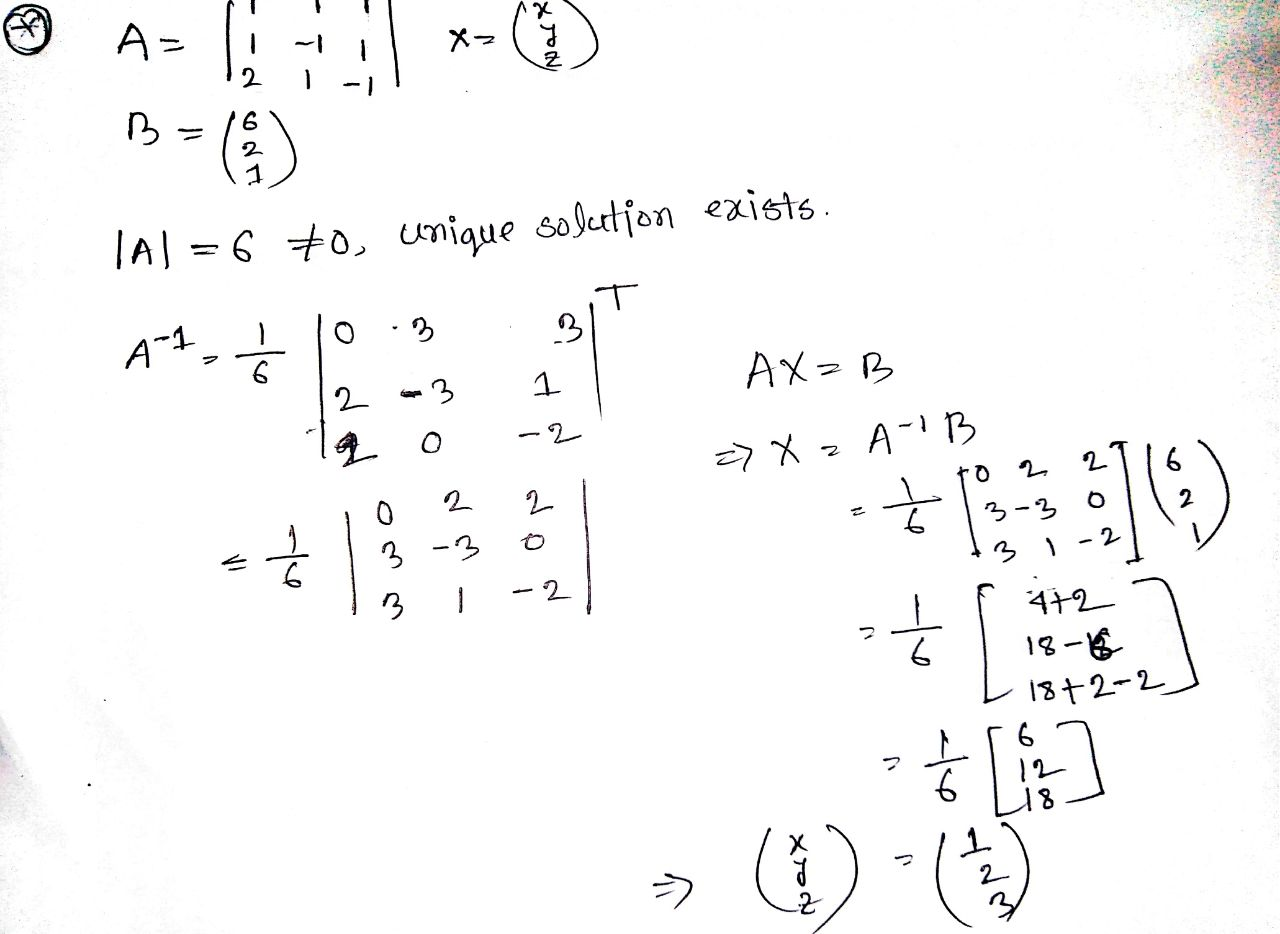
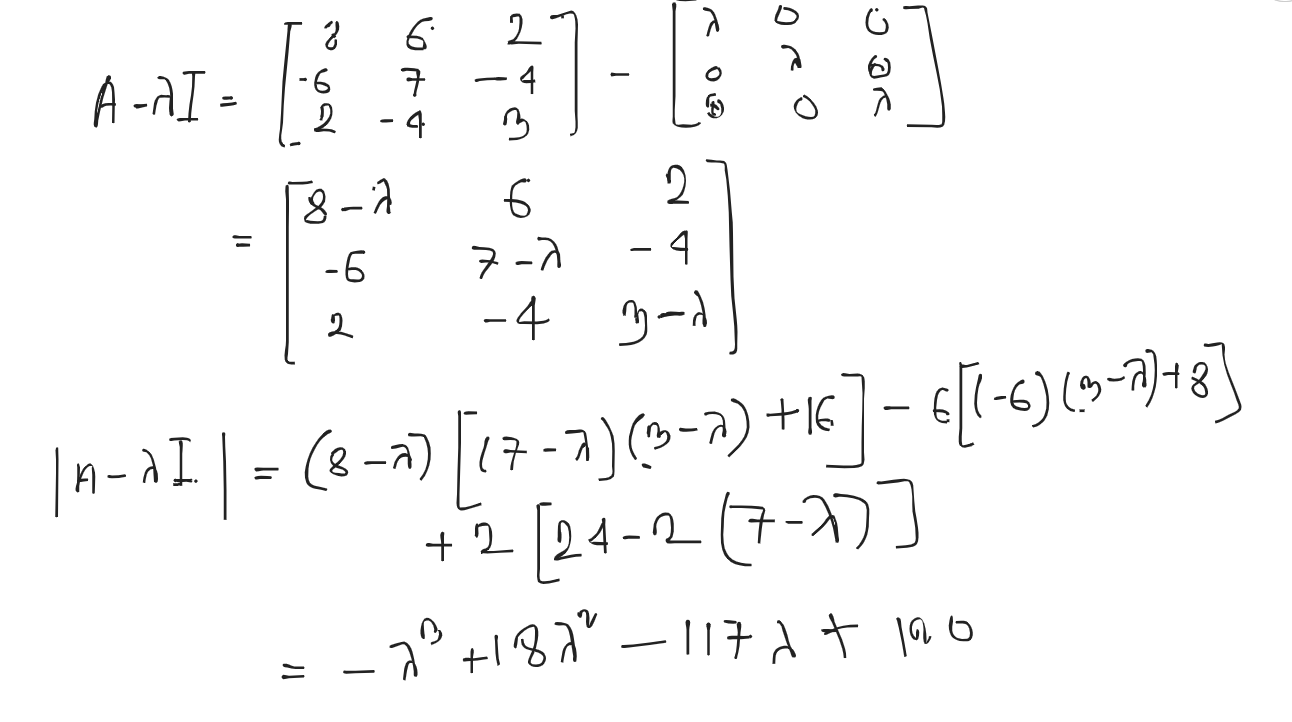
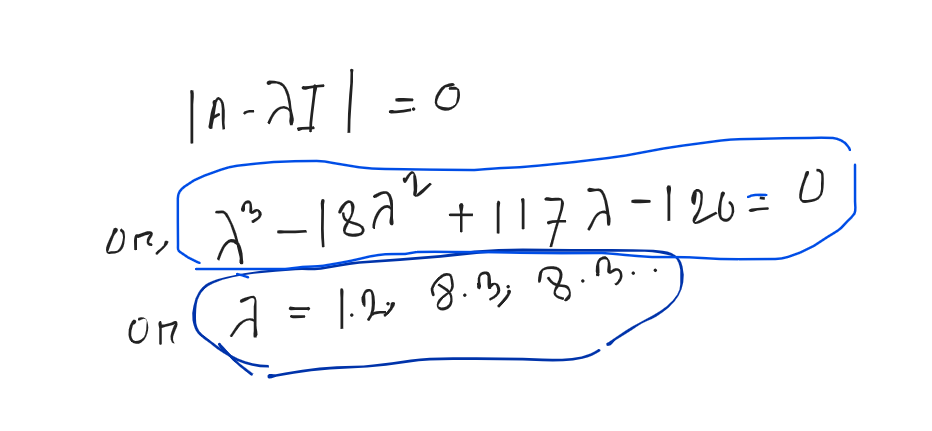
Question:

💡

Steps:
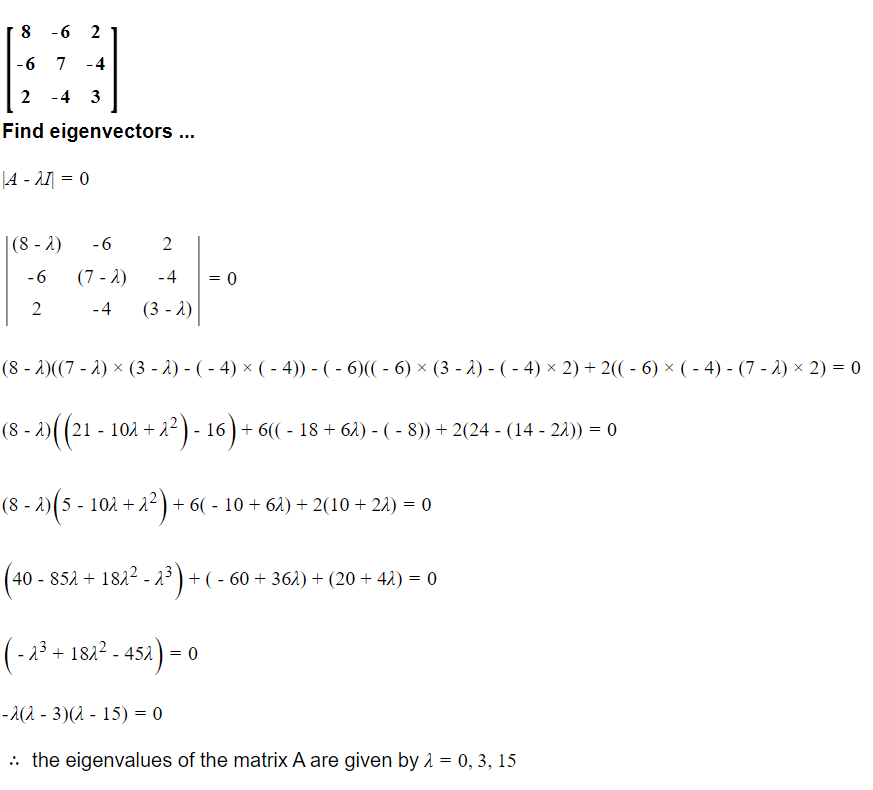
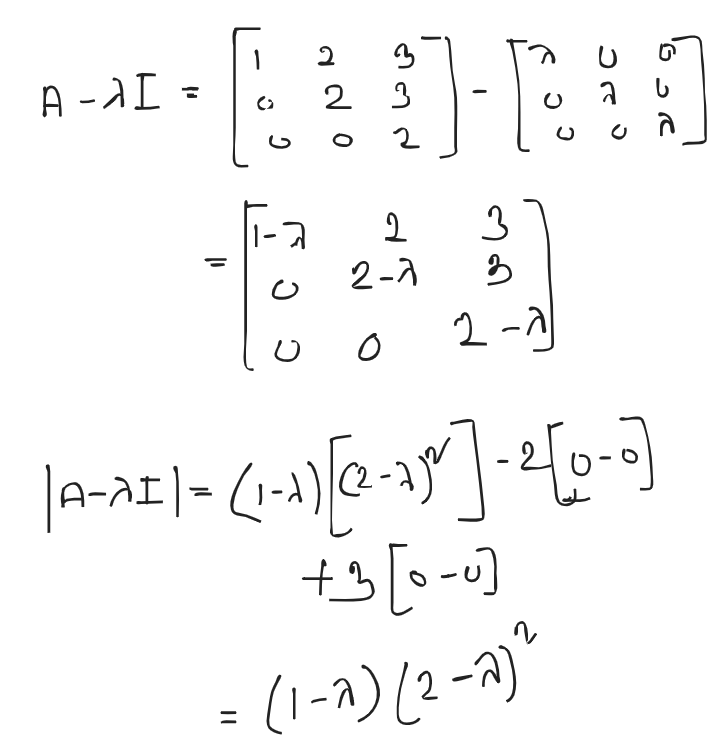
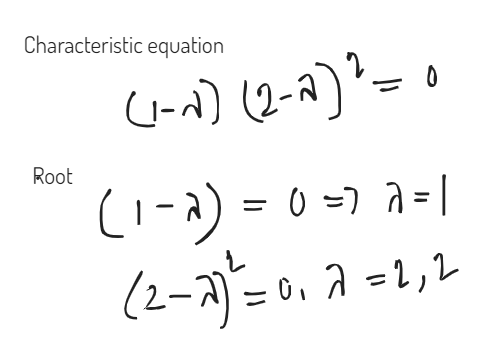
1) Eigen Value

(\lambda)

2) Eigen Vector

(V{_1}, V{_2})

3) Model Matrix

P = [V{_1} \space\space\space\space\space\space V{_2}]

4) Diagonalized Matrix :

P^{-1}AP

💡

Cayley Hamilton Theorem
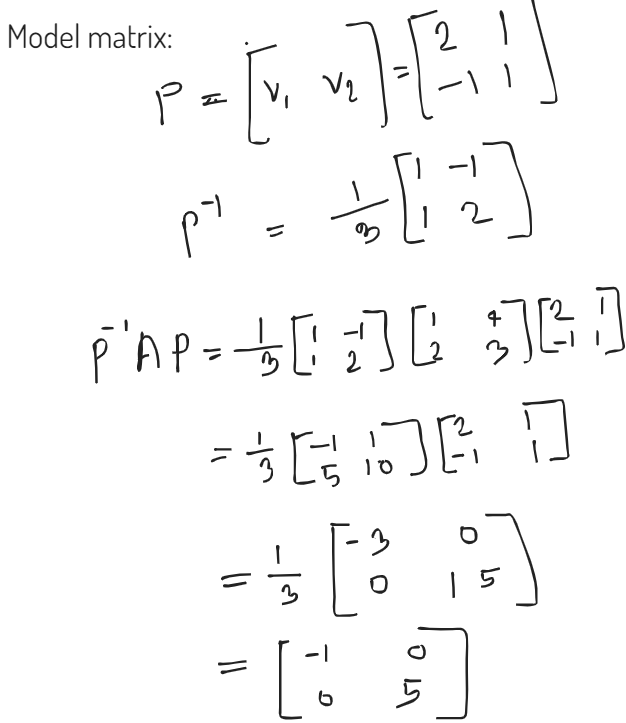
Cayley Hamilton theorem states that every square matrix satisfies it’s own equation.

Verification
1) Figure out the characteristics equation
2) Replace A (matrix) instead of

\lambda

3) Add an identity matrix with constant

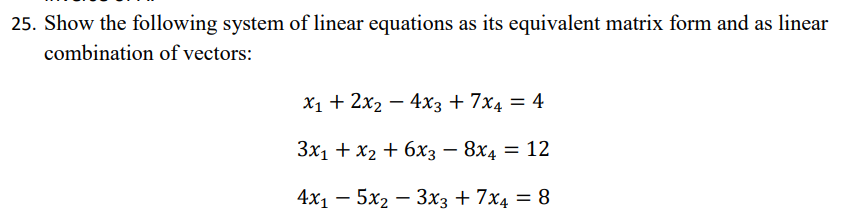
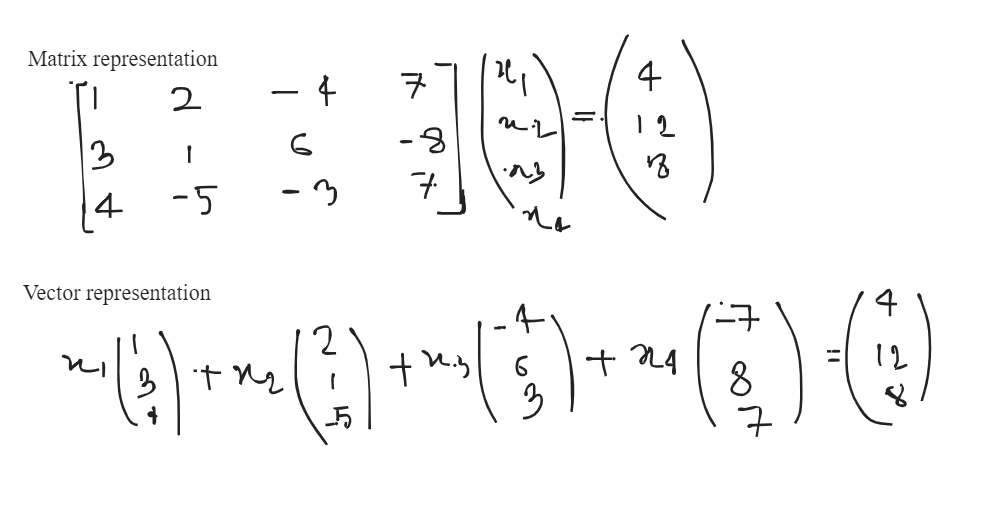
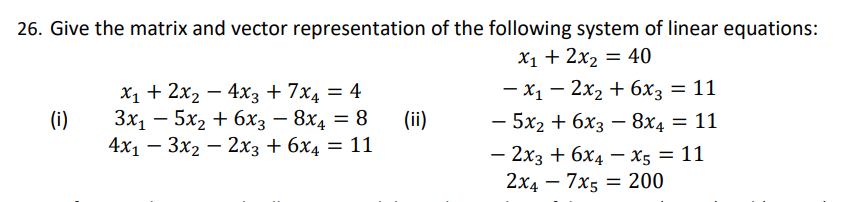
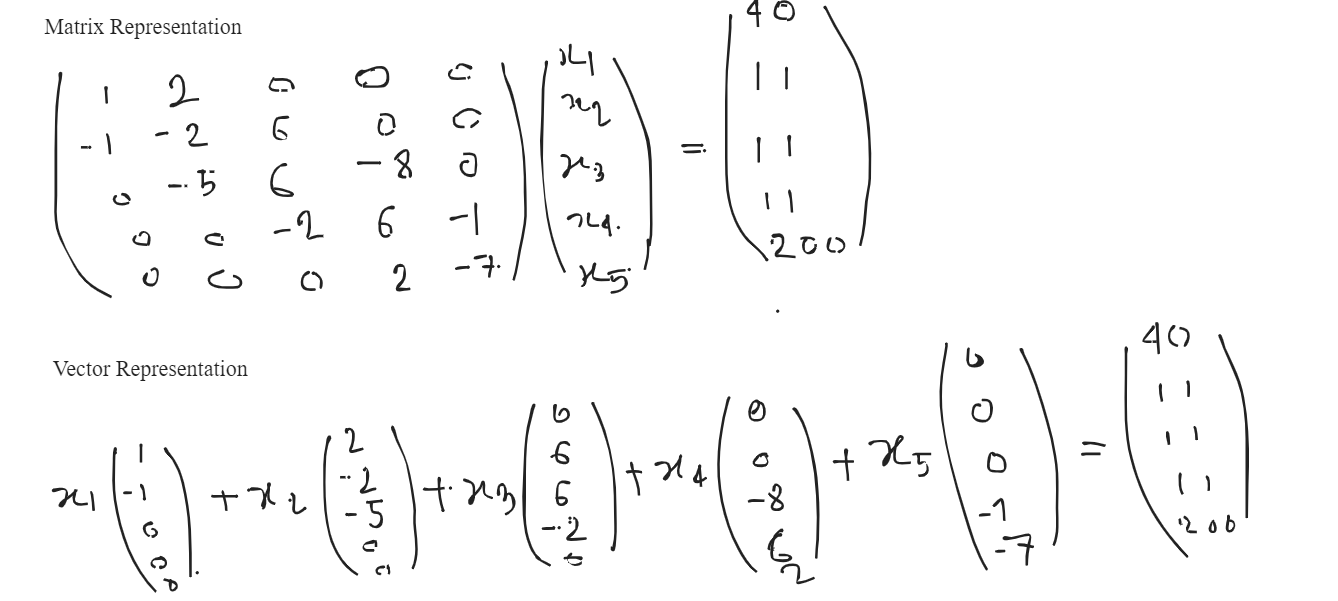
Equal Vector: Equal vectors are defined as two vectors having same magnitude and direction

Null Vector: A directionless vector whose magnitude is zero is called a null vector

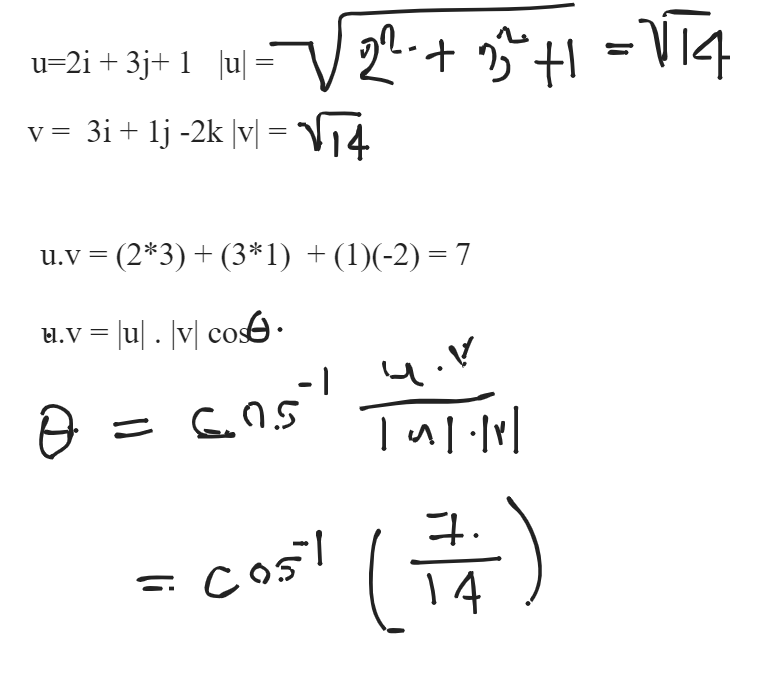
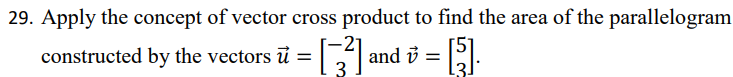
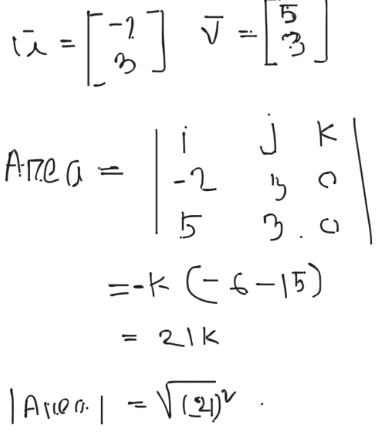
$AA^T = A^TA \not= I$ , not orthogonal

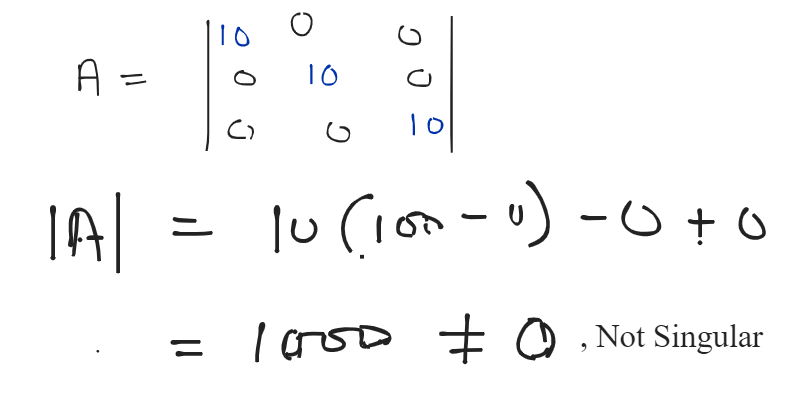
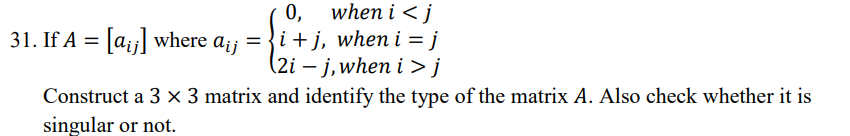
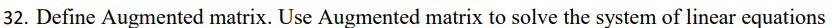
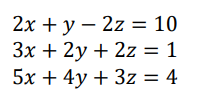
An augmented matrix is a matrix formed by combining the columns of two matrices to form a new matrix.

💡

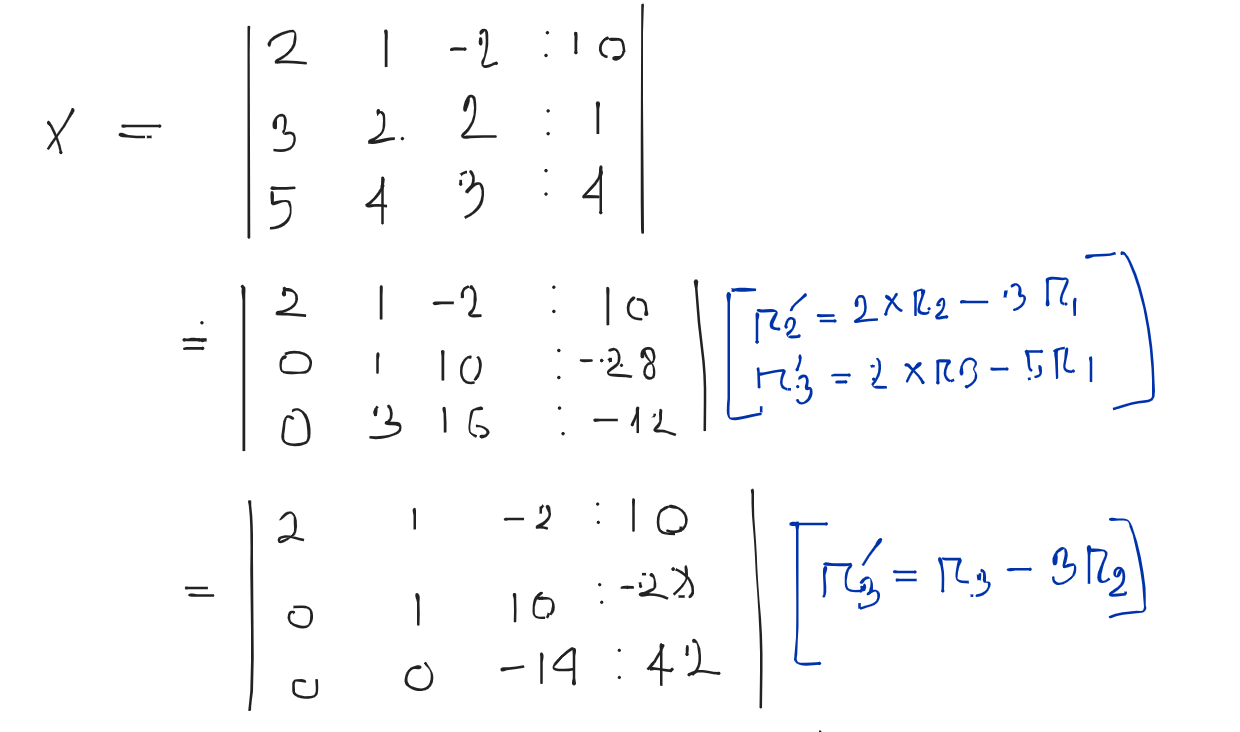
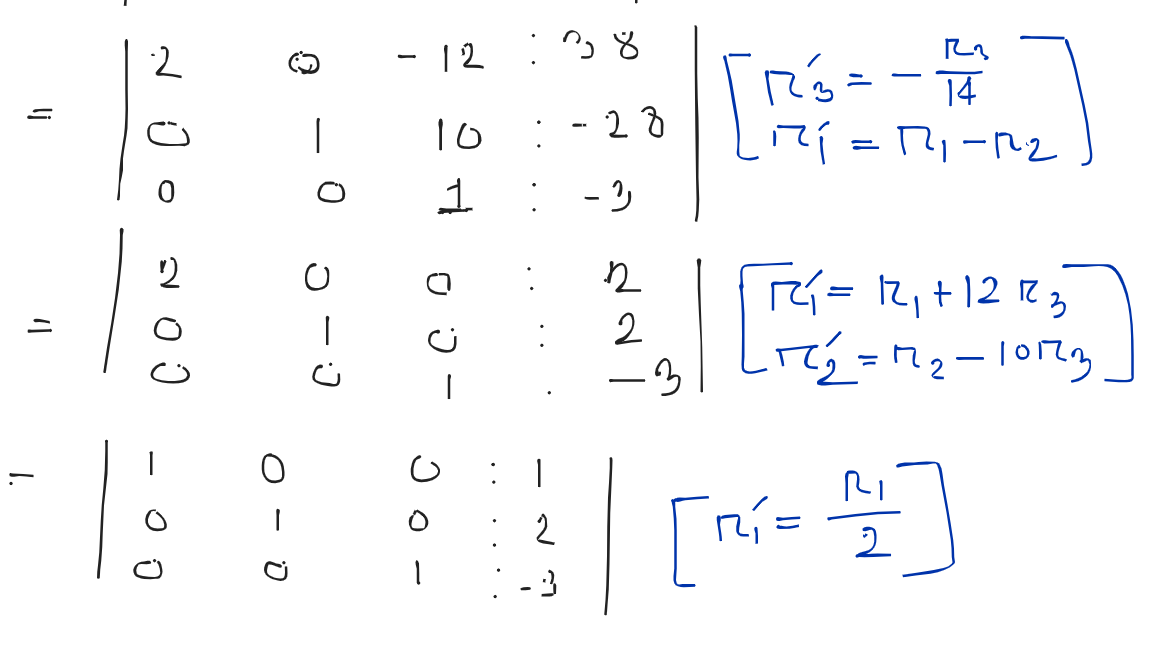
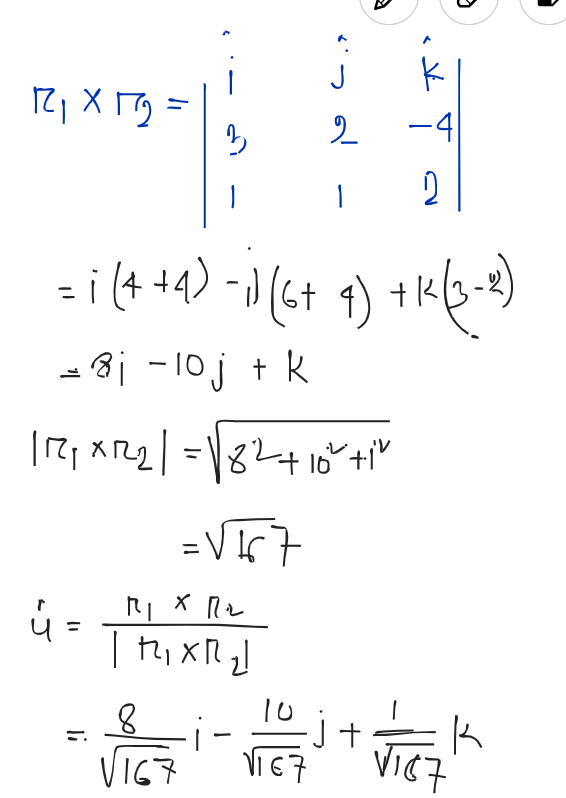
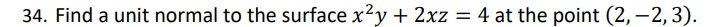
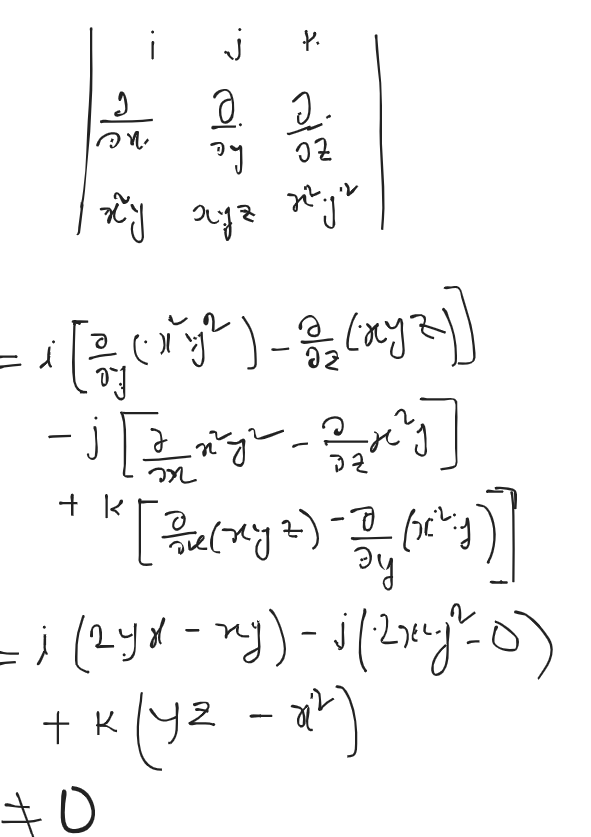
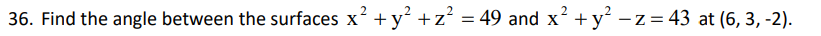
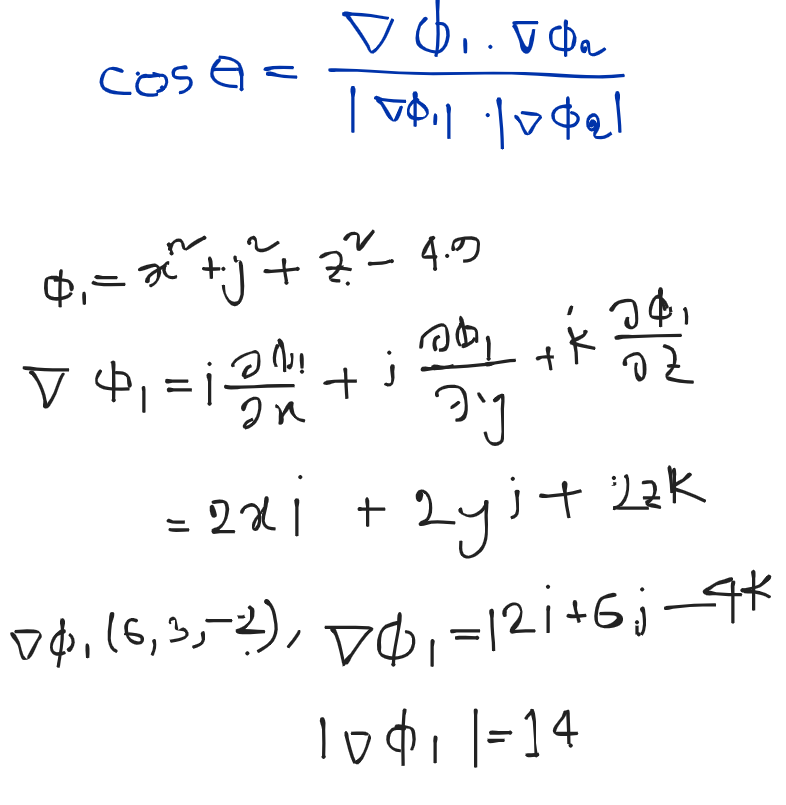
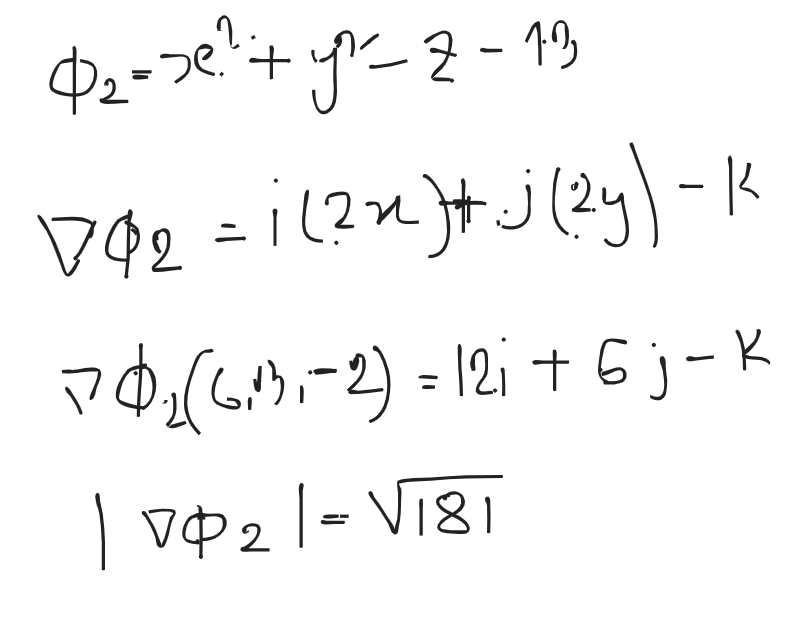
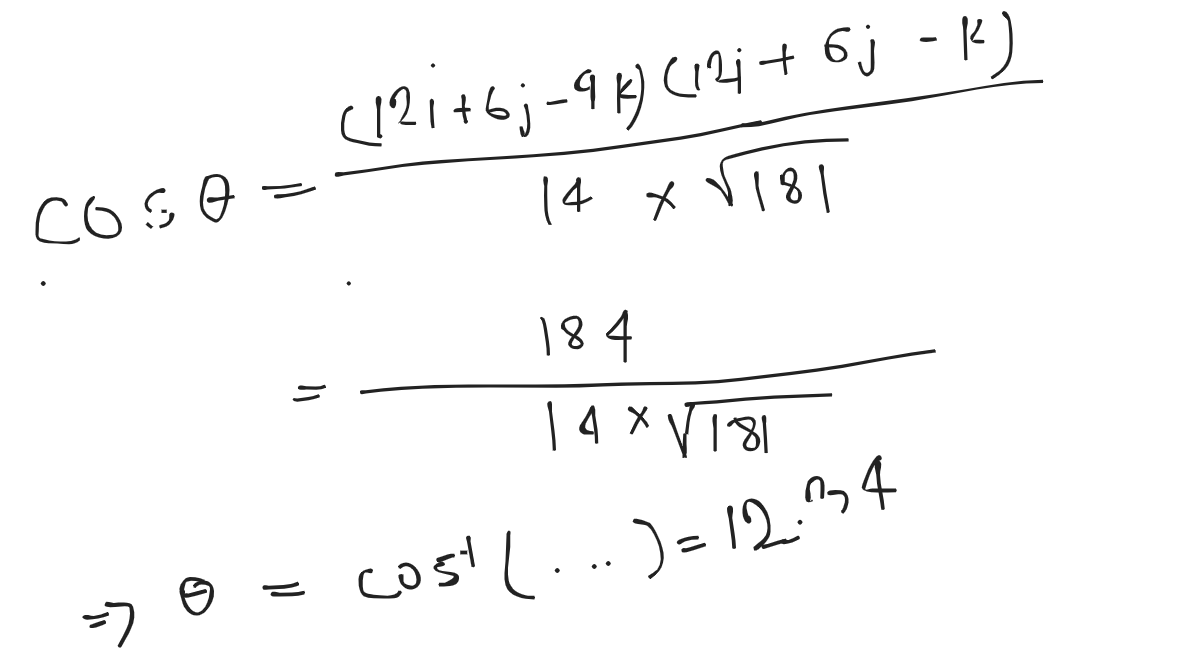
Curl (F) = 0 → Conservative & Irrotational

Final List

Write down three vector operators gradient, divergence and curl.
Gradient: The gradient of a function is defined to be a vector field. It denotes the direction of greatest change of a scalar function .The gradient of a scalar-valued function $f(x,y,z)$ is the vector field
$grad\space f =$ $\Delta f = \frac{\delta f}{\delta x} i + \frac{\delta f}{\delta y} j + \frac{\delta f}{\delta z} k$
$\Delta f$ is a vector valued function, but $f$ is not.

Divergence: Divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. The divergence of a vector field $F(x, y,z)$ is the scalar-valued function
$div F = \Delta. F = \frac{\delta F_1}{\delta x} + \frac{\delta F_2}{\delta y} + \frac{\delta F_3}{\delta z}$
$F$ is vector-valued function but, $div F$ is not.

Curl: Curl is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl of a vector field $F(x,y,z)$ is the vector field
$curl \space F = \Delta \times F$
$F$ and $curl \space F$ are both vector-valued function.

Show that the divergence of the curl of a vector field A is zero.

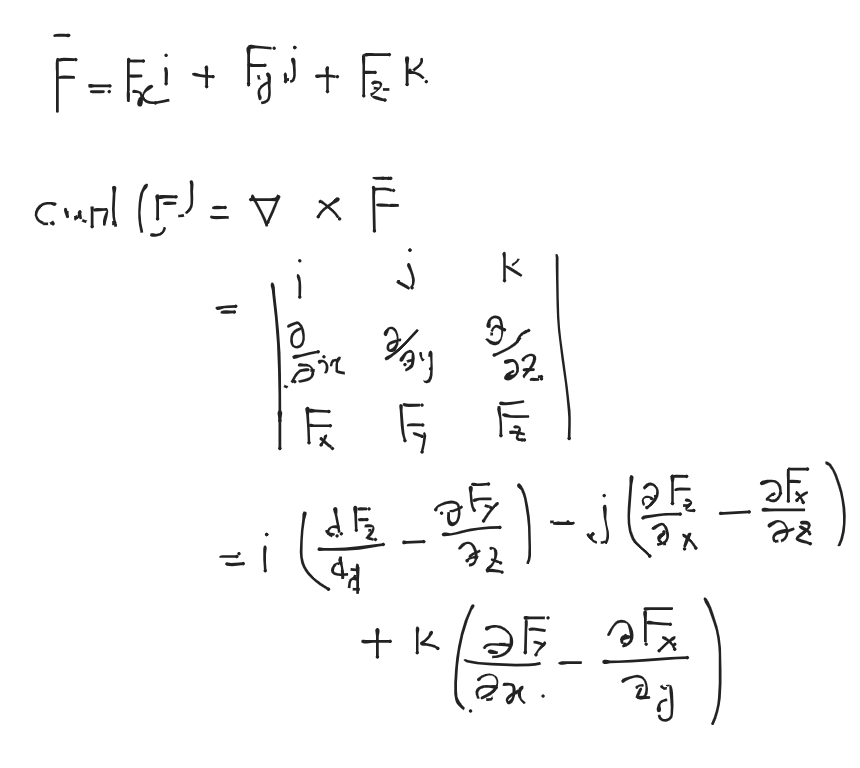
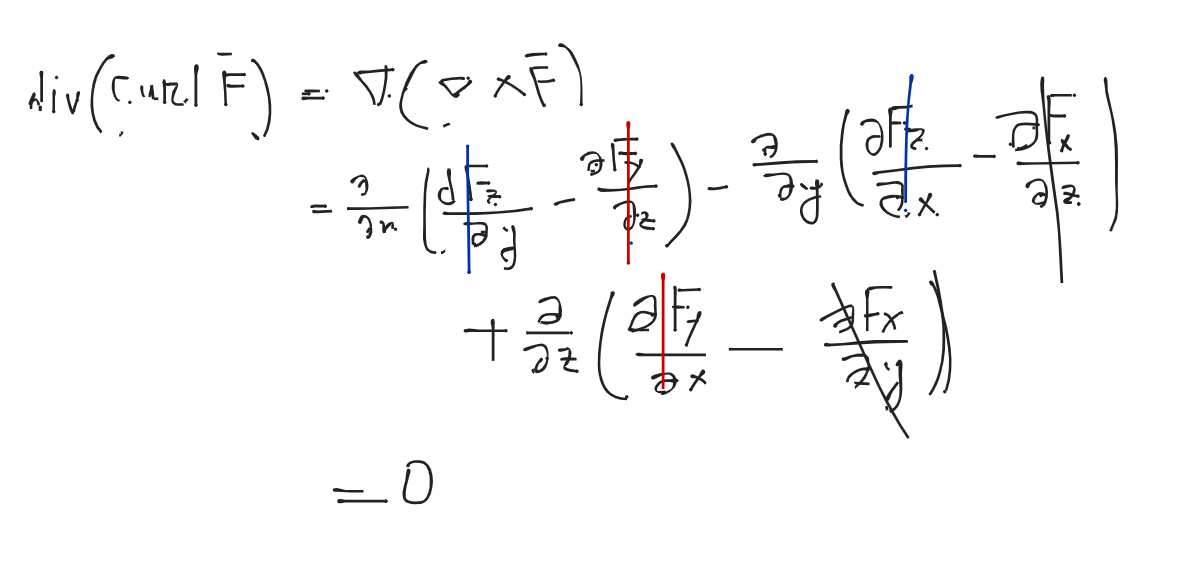
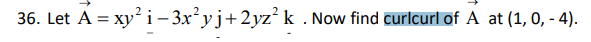
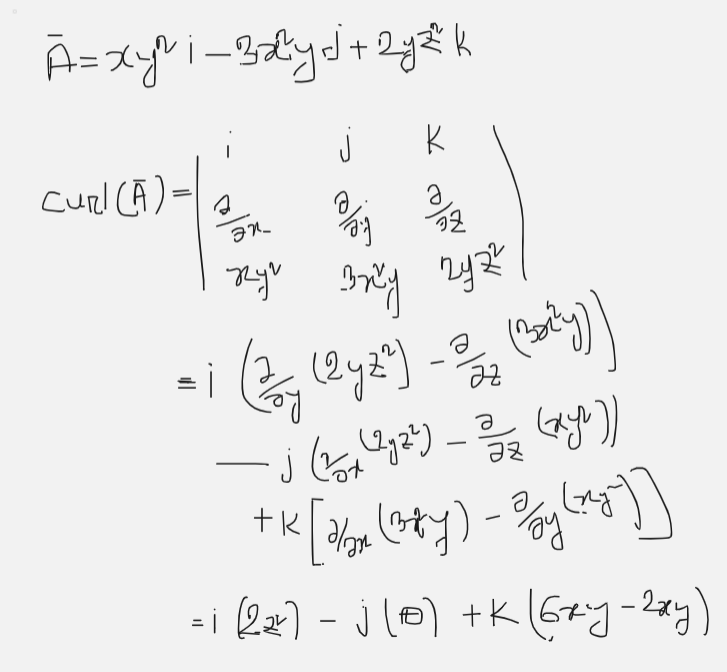
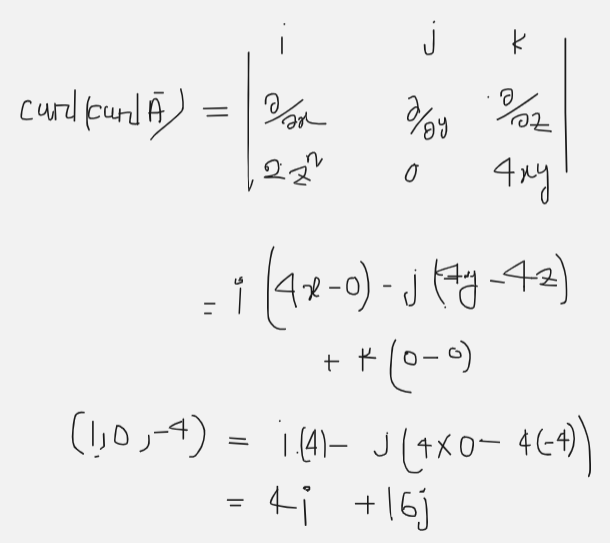
An inner product is a generalization of the dot product. In a vector space, it is a way to multiply vectors together, with the result of this multiplication being a scalar.